构造法：数形结合的桥梁

实现数形结合，常与以下内容有关：①实数与数轴上的点的对应关系；②函数与图像的对应关系；③曲线与方程的对应关系；④以几何元素和几何条件为背景建立起来的数学概念，如三角函数、向量等；⑤所给的等式或代数式的结构含有明显的几何意义，如斜率、截距、距离等.数转化为形或形转化为数有时并非很容易，常常需要借助“构造法”，即通过对等式或代数式的分析构造出相匹配的几何图形，通过几何图形相应元素的关系使原问题解决，或从所给的形中提炼出数量关系，通过运算或推理使原问题解决，总而言之，“构造法”是数形结合的桥梁.

例1　在平面直角坐标系中，O为原点，动点D满足则的最大值为________.

解题策略　本题条件是给出3个定点和1个动点D.动点D满足可知其轨迹是确定的.求的最大值解题思路有两个方向.一是利用代数的方法，构造目标函数，而构造目标函数可以引入角为参数，由于点D在以C为圆心1为半径的圆上，可运用圆的参数方程利用三角函数求解，也可引进坐标参数求解.即求出向量模长的表达式，从而转化为求函数的最值；二是利用向量的几何意义.运用向量的几何性质即构造图形、利用不等式性质求解.构造的量模型无疑是一种具有创造性的解法.

解法一　(引进角参数建立目标函数)由可知，点D在以点C(3，0)为圆心，1为半径的圆上，设D(3+cosθ,sinθ),θ∈[0,2π],则

故

则

解法二　(引进坐标参数建立目标函数)由可知，点D在以点C(3，0)为圆心，1为半径的圆上，设D(x,y)，则

故它表示圆C上的点到点E(1，的距离，

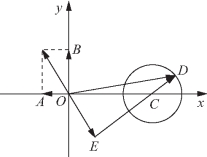
图5-36

解法三　(构建向量模型)由已知得如图5-36所示.论

则

由图5-36可知,

解法四　(运用向量的三角不等式)

已知故

,当且仅当向量与同向时等式成立.

故的最大值为

例2　已知α，β，γ均为锐角，有cos2α+cos2β+cos2γ=1,求证：

解题策略　由于题设正是长方体的一个重要性质：若长方体的一条体对角线与从一端点出发的三条棱所成角为α，β，γ,则cos2α+cos2β+cos2γ=1.所以构造长方体，运用三角函数的定义，结合基本不等式问题迎刃而解.

证明　由已知条件作一长方体ABCD-A1B1C1D1,使∠C1AD=α,∠C1AB=β,∠C1AA1=γ，如图5-37所示.

图5-37

设AD=a,AB=b,AA1=c,则

由于

从而有

当且仅当a=b=c时取等号，故

例3　(1)试求函数的最小值;

(2)设a，b都是实数，试求：的最小值.(www.xing528.com)

解题策略　数形结合思想的核心是：“以形助数，以数解形”，使复杂问题简单化、抽象问题具体化，从而找到解题思路，使问题得到解决，以形助数常借助于数轴、函数图像、单位圆、数式的结构特征、解析几何方法、向量知识等；以数解形常借助于几何轨迹所遵循的数量关系、运算结果与几何定理的结合等.第(1)问粗看似乎无从入手，若能构造出抛物线方程，使问题转化为抛物线上动点到两个定点的距离之和，利用抛物线的定义、结合平面上两点距离的线段为最短，则问题可顺畅解出.第(2)问，根据数式的结构特征，S可看作两点距离的平方，而要求其最小值，则必须搞清这两个动点在何种曲线上，结合图形则其最小值轻松可得.正如宋朝诗人杨万里的诗句：“莫问早行奇绝处，四方八面野香来.”一旦掌握了数与形之间的辩证关系，就会消除解题过程中的心理障碍，不断提高解题能力.

图5-38

图5-39

解：(1)构造动点P(x,x2),则P的轨迹方程为y=x2,设则F正好为抛物线x2=y的焦点，抛物线准线方程为

如图5-38所示，过点P作PH⊥l于H，过点A作AH0⊥l于H0，交抛物线于P0，故有当且仅当P在P0处时，f(x)取得最小值

(2)设则S为A，B两点间距离的平方，而点A在圆x2+y2=3的x轴上部分，点B在双曲线的x轴下部分，如图5-39所示.要使最小，则点A，B分别位于点或点即当或

例4　对于具有相同定义域D的函数f(x)和g(x),若存在函数h(x)=kx+b(k,b为常数)，对任意的正数m，存在相应的x0∈D,使得当x∈D且x>x0时，总有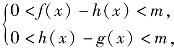 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”，给出定义域均为D={x|x>1}的4组函数如下：

①

②

③

④

其中，曲线y=f(x)与y=g(x)存在“分渐近线”的是(　　).

A.①④　　　　　　B.②③　　　　　　C.②④　　　　　　D.③④

解题策略　本例是新概念题，主要考查对新概念的理解以及函数的图像与性质.直接运用新概念中的不等式组解，难度较大，借助于图像是解决问题的最好方法，同时考查学生思维能力及创新意识.本例突出了数形结合的思想，在运用图像之前，对解析式应作些变形(这也是一种“构造”)，使之朝基本函数靠近，从而使函数图像容易作出.

解：由题意知x→+∞时，f(x)与g(x)有相同的渐近线，且f(x)与g(x)图像分别在渐近线的两侧.

①的图像如图5-40所示，当x>1时，两图像无渐近线，不合题意.

②的图像如图5-41所示，f(x)与g(x)有相同的渐近线h(x)=2且f(x)与g(x)分别在渐近线两边，符合题意.

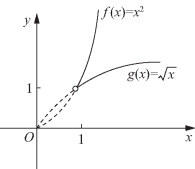
图5-40

图5-41

③的图像如图5-42所示.当x>1时f(x)与g(x)的图像有共同的渐近线h(x)=x,但f(x)与g(x)的图像在渐近线同侧，不合题意.

④的图像如图5-43所示，当x→+∞时，的渐近线为y=2(x-1).由图像知f(x)与g(x)有共同的渐近线h(x)=2(x-1)，且f(x)与g(x)的图像分别在渐近线两侧，符合题意，故选C.

图5-42

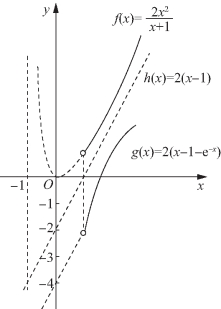
图5-43