数形兼顾与相互补充的重要性

数形结合，即用形研究数，用数研究形，相互结合，相互补充，使问题变得直观、简捷、思路易寻，从形到数主要是指分析图形、发现规律，得到有用结论，即“识图→用图”；从数到形则是从观察“数”的结构特征入手，联想与想象其几何特征，并由静而动，结合作图以便直观地发现解题思路.对于某些较为复杂的数学问题必须做到数形兼顾，反复转换，如“数→形→数”或“形→数→形”，甚至有多个反复，交替使用.

例1　已知a>0,a2-2ab+c2=0,bc>a2,试比较实数a，b，c的大小关系.

解题策略　本例可转化为函数图像与不等式表示的区域，以形助数；然而光靠图形尚不能比较a，b，c的大小，还需要作差比较，即以数辅形.数形结合的思想方法的实质是将抽象的数学语言和直观图结合起来，通过对图形的处理，发挥直观对抽象的支柱作用.通过对数与式的运算和变换，将图像的特征及几何关系刻画得更准确、更精细，这样就可以使抽象概念和具体形象相互联系、相互补充、相互转化、相互作用，最终解决问题.

解：由则点(c,b)是抛物线上的点，由bc>a2,可知(c,b)是xy=a2上方的点，故满足的点(c,b)应为阴影内的抛物线上除去(a,a)的点，∴c>a,b>a,这就是数到形的转变的结果(如图5-30所示).

图5-30

而b，c的大小关系要用代数的方法解决.

例2　已知集合A={(x,y)|y2=x+1,x,y∈R},B={(x,y)|4x2+2x-2y+5=0,x,y∈R},C={(x,y)|y=kx+b,x,y∈R},是否存在正整数k和b使得(A∪B)∩C=∅？若存在，求出k和b的值；若不存在，请说明理由.

解题策略　数形结合的思想简言之就是代数问题几何化、几何问题代数化，充分体现图形的直观性、代数推理的合理性，解题时注意不能用图形的直观代替严密的逻辑推理，本例的解题策略归结起来就是：数形兼顾求参数值.

解：画出4x2+2x-2y+5=0和y2=x+1的图像，它们分别与y轴正半轴相交于点和(0，1)(如图5-31所示).

图5-31

要使(A∪B)∩C=∅,就是要直线与上述两条抛物线均无交点，这时

而且方程组

和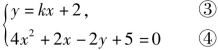　均无实数解.

把①代入②得k2x2+(4k-1)x+3=0.

把③代入④得

由得

因此存在正整数k=1,b=2满足(A∪B)∩C=∅.

例3　已知f(x)是定义在区间(-∞,+∞)上以2为周期的函数，对k∈Z，用Ik表示区间(2k-1,2k+1],已知当x∈I0时，f(x)=x2.

(1)求f(x)在Ik上的解析表达式；

(2)对自然数k,求集合Mk={a|使方程f(x)=ax在Ik上有两个不相等的实数根}.

解题策略　在求出x∈Ik上的函数解析式f(x)=(x-2k)2之后与f(x)=ax联立，得方程(x-2k)2=ax，即x2-(4k+a)x+4k2=0.此方程在(2k-1,2k+1]上有两个不相等的实根，若用纯代数方程，则原问题等价于

解此不等式组求得a的取值范围，但是运算量实在太大，故不能选择这种烦琐的解法，应考虑数形结合的解法，而实现数形结合的关键是构造.可把问题转化为求y1=(x-2k)2,x∈Ik,k∈N与y=ax有两个交点时a即直线y=ax斜率a的取值范围，也可以通过分离变量，将方程转化为另一类函数模型，寻求问题的几何意义，当然，若设f(x)=x2-(4k+a)x+4k2，利用根的分布定理求解也是一种不错的选择.

解：(1)∵2是f(x)的周期，当k∈Z时，2k也是f(x)的周期.

又∵当x∈Ik时，(x-2k)∈I0,∴f(x)=f(x-2k)=(x-2k)2,

即对k∈Z,当x∈Ik时，f(x)=(x-2k)2.

(2)解法一　(转化为求直线y=ax斜率a的取值范围)(www.xing528.com)

图5-32

方程f(x)=ax,即(x-2k)2=ax有两个不等实根，x∈(2k-1,2k+1],k∈N.令y1=(x-2k)2,x∈Ik,k∈N,y2=ax,如图5-32所示，在同一坐标系中分别作出y1，y2的图像，y2的图像是过原点，斜率为a的直线，方程有两个不等实根的充要条件是在图像有两个不同交点，见图5-32，当时两图像有两个不同交点.从而，原方程有两不等实根时，

解法二　(分离变量，将方程转化为函数模型，寻求问题的几何意义)

图5-33

联立得令作这两个函数的图像,如图5-33所示.图像有两个不同交点的充要条件是即

解法三　(用根的分布理论求解)

图5-34

令f(x)=x2-(4k+a)x+4k2,则问题转化为f(x)的图像在区间(2k-1,2k+1]上与x轴有两个不同的交点，如图5-34所示，其充要条件是

解得

即

例4　过抛物线x2=2py(p>0)的焦点作斜率为1的直线与该抛物线交于A，B两点，A，B在x轴上的正射影分别为C，D,若梯形ABDC的面积为则p=________.

解题策略　本例是典型的圆锥曲线焦点弦问题，可以直接运用代数的方法解，即联立方程组与韦达定理结合是常规思路，但是也可以数形结合，这是因为焦点弦问题必须考虑圆锥曲线的几何特征，借助几何法解题较为简单，可起到事半功倍的效果.

解法一　直线AB方程为设A(x1,y1),B(x2,y2).

由得x2-2px-p2=0,∴x1+x2=2p,x1x2=-p2.

故S

又得p2=4,又p>0,∴p=2.

图5-35

解法二　如图5-35所示，由几何关系，设直线AB的倾斜角为θ,根据抛物线定义，

又∵S

∵直线AB斜率为将代入得，得p2=4.又p>0,∴p=2,故填入2.