以形助数,即借助形的直观性来阐明数之间的联系,由数想形时,要注意“形”的准确性,这是数形结合的基础,以形助数常用的有:借助数轴;借助函数图像;借助单位圆;借助数式的结构特征寻找内在的几何关系;借助于解析几何方法.
以形助数离不开作图,作图既要放眼整体,又要关注局部,特别要关注关键细节处,并从运动变化的角度观察图形(如解析几何中直线倾斜角与斜率的变化,直线的截距的变化,点到直线距离的变化等),防止图形选择不当而掩盖问题的本质,防止图形的直观掩藏了深入的理性思考,防止由直观得出的并不一定准确的结论代替严谨论证.
例1 (1)对a,b∈R,记![]() 则函数
则函数![]() ( ).
( ).
A.有最大值![]() 无最小值 B.有最大值
无最小值 B.有最大值![]() 无最小值
无最小值
C.有最小值![]() 无最大值 D.有最小值
无最大值 D.有最小值![]() 无最大值
无最大值
(2)已知两条直线l1:y=m和![]() 与函数y=|log2x|的图像从左至右相交于点A,B,l2与函数y=|log2x|的图像从左至右相交于C,D,记线段AC和BD在x轴上的投影长度分别为a,b,当m变化时,
与函数y=|log2x|的图像从左至右相交于点A,B,l2与函数y=|log2x|的图像从左至右相交于C,D,记线段AC和BD在x轴上的投影长度分别为a,b,当m变化时,![]() 的最小值为( ).
的最小值为( ).
![]()
![]()
解题策略 第(1)问,对于求分段函数最值问题,可在相应定义域内作出分段函数的图像,借助函数图像直观地得出函数的最大值和最小值或判断无最值.第(2)问考查对数函数图像与性质的综合应用,理解投影的概念并能把问题转化为基本不等式求最值是解决问题的关键.
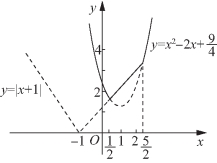
图5-18
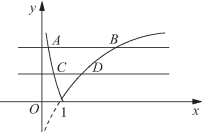
图5-19
解:(1)函数![]() 是两个函数y=|x+1|与y=x2-
是两个函数y=|x+1|与y=x2-![]() 同一个x取得的两个函数值的较大的值,在同一直角坐标系中作函数y=|x+1|与函数
同一个x取得的两个函数值的较大的值,在同一直角坐标系中作函数y=|x+1|与函数![]() 的图像,函数f(x)的图像为图中实线部分(如图5-18所示).令
的图像,函数f(x)的图像为图中实线部分(如图5-18所示).令![]() 得
得![]() 或
或![]() 由图像可知,当
由图像可知,当![]() 时,f(x)的最小值为
时,f(x)的最小值为![]() 故f(x)有最小值
故f(x)有最小值![]() 但没有最大值,故选C.
但没有最大值,故选C.
(2)在同一坐标系中作出![]() 的图像如图5-19所示,由|log2x|=m,得
的图像如图5-19所示,由|log2x|=m,得![]() 得
得![]() 依照题意得a=|x1-x3|,b=|x2-x4|得
依照题意得a=|x1-x3|,b=|x2-x4|得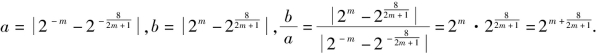
因为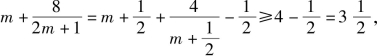 所以
所以![]() 故选B.
故选B.
例2 (1)求![]() 的最大值与最小值;
的最大值与最小值;
(2)已知x2+y2≤4,且x≥0,求![]() 的最大值与最小值.
的最大值与最小值.
解题策略 第(1)问,根据![]() 和
和![]() 形式上的特点,构造动点A(sinx,-5sinx),定点B(3,2),则原问题求y的最值转化为求kAB的最值.这就是通常所说的“图形的构造”,是数形结合思想的抓手之一;第(2)问,x2+y2≤4(x≥0)表示半圆域,
形式上的特点,构造动点A(sinx,-5sinx),定点B(3,2),则原问题求y的最值转化为求kAB的最值.这就是通常所说的“图形的构造”,是数形结合思想的抓手之一;第(2)问,x2+y2≤4(x≥0)表示半圆域,![]() 表示半圆域上的动点P(x,y)与定点A(-1,-4)连线的斜率,问题迎刃而解.
表示半圆域上的动点P(x,y)与定点A(-1,-4)连线的斜率,问题迎刃而解.
解:(1)据斜率公式![]() 构造两个点,即A(sinx,-5sinx)、B(3,2).
构造两个点,即A(sinx,-5sinx)、B(3,2).
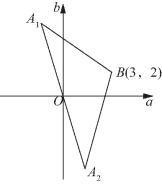
图5-20
把点A(sinx,-5sinx)视为直角坐标平面aOb内的一个动点,这时![]() 由此可得b=-5a(-1≤a≤1),如图5-20所示.b=-5a(-1≤a≤1)的图像是线段A1A2,端点A1,A2的坐标分别是(-1,5)和(1,-5),点A在线段A1A2上移动,直线A1B的斜率为
由此可得b=-5a(-1≤a≤1),如图5-20所示.b=-5a(-1≤a≤1)的图像是线段A1A2,端点A1,A2的坐标分别是(-1,5)和(1,-5),点A在线段A1A2上移动,直线A1B的斜率为![]() 直线A2B的斜率为
直线A2B的斜率为![]()
y刚好是直线AB的斜率,
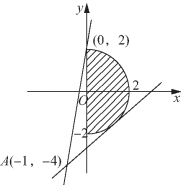
图5-21
∴y的最大值为![]() 最小值为
最小值为![]()
(2)如图5-21所示,不等式x2+y2≤4(x≥0)表示半圆域,设![]() 表示半圆域上的点(x,y)与点(-1,-4)连线的斜率,当直线过点(0,2)时,有
表示半圆域上的点(x,y)与点(-1,-4)连线的斜率,当直线过点(0,2)时,有![]() 当直线在圆的切线位置时,k值最小,由点(0,0)到切线的距离等于半径,得
当直线在圆的切线位置时,k值最小,由点(0,0)到切线的距离等于半径,得![]()
例3 (1)已知平面向量![]() 满足
满足![]() 且
且![]() 与
与![]() 的夹角为120°,则
的夹角为120°,则![]() 的取值范围是________;(https://www.xing528.com)
的取值范围是________;(https://www.xing528.com)
(2)设抛物线y2=2x的焦点为F,过点![]() 的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,|BF|=2,则△BCF与△ACF的面积之比
的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,|BF|=2,则△BCF与△ACF的面积之比![]()
![]()
解题策略 第(1)问,如图5-22所示,易知点C在圆弧上运动且∠ACB=60°,在△ABC中结合正弦定理及正弦函数的有界性可得![]() 的取值范围;第(2)问,应结合图形,将面积比转化为线段长度之比,再根据抛物线定义转化为坐标运算.
的取值范围;第(2)问,应结合图形,将面积比转化为线段长度之比,再根据抛物线定义转化为坐标运算.
解:(1)令![]() 如图5-22所示,
如图5-22所示,![]() 点C在圆弧上运动,∠ACB=60°.
点C在圆弧上运动,∠ACB=60°.
设∠ABC=θ,由正弦定理知![]()
![]() 当θ=90°时取最大值.
当θ=90°时取最大值.
![]()
(2)如图5-23所示,设点A(xA,yA)、点B(xB,yB),由题知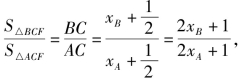 且
且![]()
由A、B、M三点共线有![]() 即
即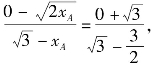 故xA=2.
故xA=2.
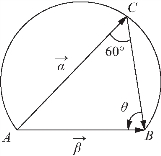
图5-22
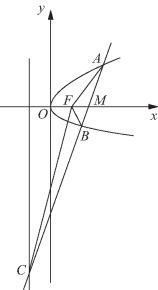
图5-23
![]() 故选A.
故选A.
例4 已知以T=4为周期的函数 其中m>0,若方程3f(x)=x恰有5个实数解,则m的取值范围为( ).
其中m>0,若方程3f(x)=x恰有5个实数解,则m的取值范围为( ).
![]()
![]()
![]()
![]()
解题策略 本题可构造两个函数,通过两个函数的图像交点的个数为5来探求m的取值范围,然而以形助数往往是粗略的,临界状态不一定很明了,还应结合代数运算,即通过解方程组,运用方程理论作进一步探索.数形结合关键在结合,不但要以形助数,还要以数辅形,这样解才是完整的.
解:方程3f(x)=x可化为![]() 构造函数
构造函数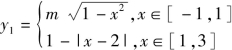 和
和![]()
当-1≤x≤1时为![]() 的上半部分;当1<x≤2时为y=x-1;当2<x≤3时为y=-x+3,它们在一个周期[-1,3]内恰有3个交点.
的上半部分;当1<x≤2时为y=x-1;当2<x≤3时为y=-x+3,它们在一个周期[-1,3]内恰有3个交点.

图5-24
根据周期性作出函数其他部分的图像,如图5-24所示,![]() 为一条过原点的直线,要使它们符合题意,需要使
为一条过原点的直线,要使它们符合题意,需要使![]() 与曲线C2有两个交点,与C3没有交点.
与曲线C2有两个交点,与C3没有交点.
由题意知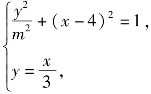 得
得![]()
![]() 得
得![]()
由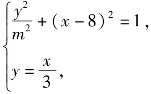 得
得![]()
![]() 得
得![]()
故![]() 故选B.
故选B.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




