数形结合是根据数量与图形之间的对应关系,通过数与形的相互转化来解决问题的一种重要思想方法,也是一种智慧的解题技巧,数形结合的思想简言之就是代数问题几何化,几何问题代数化,即“以形助数,以数解形”,使复杂问题简单化,抽象问题具体化,可以帮助我们找到解决问题的思路和方法.
由“形”到“数”的转化,往往比较明显,而由“数”到“形”的转化则需要转化的意识,因此,数形结合思想的使用往往偏重于由“数”到“形”的转化.
例1 已知函数f(x)=|x2+3x|,x∈R,若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为________.
解题策略 所给的方程既含参数,又含绝对值符号,恰有4个互异的实数根,求参数的取值范围,用代数的方法直接解是困难的,只有通过转化为不同函数的图像交点问题才能获得结果,难点当然是如何把方程问题转化为函数问题(有时转化的方法不唯一),关键点是在定义域范围内较为精确地画出函数的图像,本题中的方程可转化为函数y=a|x-1|与y=|x2+3x|有4个交点问题,也可转化为函数![]() 与y=a有4个交点问题,其中一个函数带有参数,从而构造的两个函数一动一静,直观易解.
与y=a有4个交点问题,其中一个函数带有参数,从而构造的两个函数一动一静,直观易解.
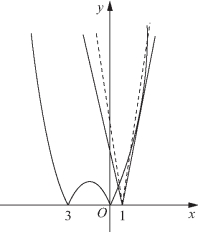
解法一 显然a>0,用数形结合的方法,分别作出函数y=a|x-1|与y=|x2+3x|的图像,两图像一动一静,如图5-2(a)所示,当y=-a(x-1)与y=-x2-3x相切时a=1,此时f(x)-a|x-1|=0恰有3个互异的实数根,显然当0<a<1时,方程有4个互异的实数根.
如图5-2(b)所示,当直线y=a(x-1)与y=x2+3x相切时,a=9,此时f(x)-a|x-1|=0恰有3个互异的实数根,当a>9时,方程有4个互异的实数根.
综上,实数a的取值范围为0<a<1或a>9.
解法二 显然![]()
令t=x-1,则![]()
![]()
![]() 如图5-3所示.
如图5-3所示.
![]() 结合图像可得0<a<1或a>9.
结合图像可得0<a<1或a>9.

(a)
(b)
图5-2

图5-3
例2 在平面内,定点A,B,C,D满足![]() 动点P,M满足
动点P,M满足![]() 则
则![]() 的最大值是( ).
的最大值是( ).
![]()
解题策略 可通过发散思维构造符合题意的图形,在新的图形背景下获得较多的解法.

图5-4
解法一 由题意,![]() 可知,D到A,B,C3点的距离相等,D是△ABC的外心,
可知,D到A,B,C3点的距离相等,D是△ABC的外心, 同理可得DA⊥BC、DC⊥AB,从而D是△ABC的垂心,∴△ABC的外心与垂心重合,因此△ABC是正三角形,且D是△ABC的中心,
同理可得DA⊥BC、DC⊥AB,从而D是△ABC的垂心,∴△ABC的外心与垂心重合,因此△ABC是正三角形,且D是△ABC的中心,![]()
∴正△ABC的边长为![]()
以A为原点,建立直角坐标系,B,C,D三点坐标分别为![]() 如图5-4所示.由
如图5-4所示.由![]() 设P点坐标为(cosθ,sinθ),其中θ∈[0,2π),而
设P点坐标为(cosθ,sinθ),其中θ∈[0,2π),而![]() 即M是PC的中点,∴点M的坐标为
即M是PC的中点,∴点M的坐标为![]() 则
则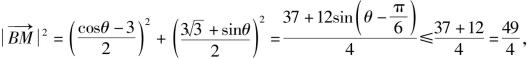 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() 故选B.
故选B.

图5-5
解法二 由![]() 知,点A,B,C在以点D为圆心的圆上,设圆的半径为r,由
知,点A,B,C在以点D为圆心的圆上,设圆的半径为r,由![]() 得r2cos∠ADB=r2cos∠BDC=r2cos∠CDA=-2,∴∠ADB=∠BDC=∠CDA=120°,代入上式得r=2.以点D为原点,以DA所在直线为x轴建立直角坐标系,如图5-5所示,易求得
得r2cos∠ADB=r2cos∠BDC=r2cos∠CDA=-2,∴∠ADB=∠BDC=∠CDA=120°,代入上式得r=2.以点D为原点,以DA所在直线为x轴建立直角坐标系,如图5-5所示,易求得![]()
由![]() 知,动点P在以A为圆心,半径为1的圆上,故可设P(2+cosθ,sinθ),其中θ∈[0,2π),又由
知,动点P在以A为圆心,半径为1的圆上,故可设P(2+cosθ,sinθ),其中θ∈[0,2π),又由![]() 知点M为PC的中点.
知点M为PC的中点.
![]() (https://www.xing528.com)
(https://www.xing528.com)
而![]()
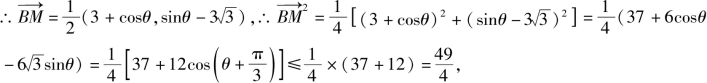 故选B.
故选B.

图5-6
解法三 如图5-6所示,![]()
∴D是△ABC的垂心,又![]()
∴△ABD≌△BCD≌△ACD,由![]()
![]()
![]() 是PC中点,取AC中点N,联结
是PC中点,取AC中点N,联结![]()
![]()
![]()
![]()
![]()
当且仅当![]() 与
与![]() 同向共线时,
同向共线时,![]() 有最大值为
有最大值为![]() 故选B.
故选B.
解法四 由题意,D是正△ABC的中心,且![]()
![]()
设![]() 由
由![]() 知M为线段PC的中点,
知M为线段PC的中点,
设M(x,y),则![]() 由
由![]() 得
得![]()
即点M的轨迹为圆![]() 圆心为
圆心为![]()
于是|BM|的最大值为![]() 故
故![]() 的最大值为
的最大值为![]()
例3 已知![]() 求函数
求函数![]() 的最小值.
的最小值.
解题策略 本题是双变量三角函数最小值的求解,结构复杂,难以直接求解,不妨借助于图形去探索,去开辟新路,核心问题就变成如何以形助数,如何把“数”的问题转化为“形”的问题,并通过对形的分析解决数的问题.
解:设![]() 且
且![]() 可得圆弧C1:x2+y2=6(x>0,y>0);
可得圆弧C1:x2+y2=6(x>0,y>0);

图5-7
又设x=3tanβ,y=3cotβ,且![]() 可得等轴双曲线一支C2:xy=9(x>0,y>0),于是函数z的几何意义为曲线C1上的点与曲线C2上的点之间距离的平方,从而“数”的问题转化为“形”的问题,如图5-7所示,设过圆心的直线y=x与曲线C1,C2分别交于A,B两点,由图知AB的平方为z的最小值,即
可得等轴双曲线一支C2:xy=9(x>0,y>0),于是函数z的几何意义为曲线C1上的点与曲线C2上的点之间距离的平方,从而“数”的问题转化为“形”的问题,如图5-7所示,设过圆心的直线y=x与曲线C1,C2分别交于A,B两点,由图知AB的平方为z的最小值,即![]()
例4 (2019年高考数学江苏卷理科第14题)设f(x),g(x)是定义在R上的两个周期函数,f(x)的周期为4,g(x)的周期为2,且f(x)是奇函数.当x∈(0,2]时, 其中k>0.若在区间(0,9]上,关于x的方程f(x)=g(x)有8个不同的实数根,则k的取值范围是________.
其中k>0.若在区间(0,9]上,关于x的方程f(x)=g(x)有8个不同的实数根,则k的取值范围是________.
解题策略 本题考查函数的图像与性质、函数与方程、直线与圆的位置关系,解题的突破点是数形结合思想的灵活应用,以形助数,首先要找到“形”,而要准确地找到“形”,则首先要把函数的性质“吃透”,只有顺顺当当地画出图形.才能精准解决“数”的问题.

图5-8
解:当x∈(0,2]时,![]() 即(x-1)2+y2=1,y≥0,即函数f(x)表示以(1,0)为圆心、1为半径在x轴上方部分的半圆,又f(x)是奇函数,且周期为4,可画出函数f(x)在(0,9]上的图像,再在同一坐标系中作出函数g(x)在(0,9]上的图像,关于x的方程f(x)=g(x)在(0,9]上有8个不同的实数根,即两个函数图像在(0,9]上有8个不同的交点.如图5-8所示.
即(x-1)2+y2=1,y≥0,即函数f(x)表示以(1,0)为圆心、1为半径在x轴上方部分的半圆,又f(x)是奇函数,且周期为4,可画出函数f(x)在(0,9]上的图像,再在同一坐标系中作出函数g(x)在(0,9]上的图像,关于x的方程f(x)=g(x)在(0,9]上有8个不同的实数根,即两个函数图像在(0,9]上有8个不同的交点.如图5-8所示.
则函数g(x)与f(x)在(0,1]的图像有2个不同的交点,当直线g(x)=k(x+2)经过点(1,1)时,![]() 当直线g(x)=k(x+2)与半圆(x-1)2+y2=1(g≥0)相切时,
当直线g(x)=k(x+2)与半圆(x-1)2+y2=1(g≥0)相切时, 解得
解得![]() (舍负),所以k的取值范围是
(舍负),所以k的取值范围是![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




