数学教育家G.波利亚指出:引入辅助元素可“使问题的概念更完整,更富于启发性,更为人所熟悉”,是个“好念头”.因此,当问题的条件和结论不易发生关系或关系不明朗时,借助辅助元素——参数为媒介,可使条件和结论联结起来,让问题变得明朗,再进行分析和综合,从而解决问题.
参数法解题的关键是恰到好处地引进参数,沟通已知和未知之间的内在联系,常用参数有:代数中的比值参数、实数参数、代数式参数等(换元法就是引入参数的典型例子);几何中常用角参数、长度参数等;解析几何中常用斜率参数、坐标参数等.
引进参数的目的是能使问题轻松获解,这是参数法的基本原则.所以,引进参数必须合理,除了要考虑问题中条件与结论的特点外,还必须注意某些量的取值范围,必要时还要对参数的变化范围进行讨论.还应提醒的是原问题并非关于参数的问题,参数并不是直接研究的对象,它只起“桥梁”和转化作用,所以当求得间接解后要倒回去确定原问题的解.
参数法解题的特点概括起来是:引入参数、参与推导、消去参数、显露结论.
参数思想在解析几何内容占有很重的分量,直线方程、曲线方程的一般形式中的字母系数都可看作参数,参数思想的熏陶与运用是这门学科的重要特色,参数法也是求轨迹方程的重要方法,应给予足够的重视.
例1 (1)已知![]() 且
且![]() 求
求![]() 的值;
的值;
(2)已知![]() 且x,y为实数,|z1|+|z2|=6,
且x,y为实数,|z1|+|z2|=6,
求f(x,y)=|2x-3y-12|的最大值和最小值;
(3)实数x,y满足4x2-5xy+4y2=5,设S=x2+y2,求![]() 的值.
的值.
解题策略 第(1)问,由条件直接消元即消去sinθ,cosθ得x,y的关系式再求![]() 的值运算量太大,若引进中间参数k,即设
的值运算量太大,若引进中间参数k,即设![]() 则很容易将条件中的sinθ,cosθ消去,再引进
则很容易将条件中的sinθ,cosθ消去,再引进![]() 则又把问题转化为t的方程,解之不难.第(2)问,把复数方程转化为椭圆标准方程,引进角参数,进一步把椭圆标准方程转化为椭圆的参数方程,又一次转化为求三角函数的最值问题.第(3)问有多种引入参数的方法,方法一:由x2+y2=S,联想到三角公式cos2α+sin2α=1,参进参数α.通过“三角换元法”将问题转化为熟悉的简单三角函数求S的最大值和最小值,还可由
则又把问题转化为t的方程,解之不难.第(2)问,把复数方程转化为椭圆标准方程,引进角参数,进一步把椭圆标准方程转化为椭圆的参数方程,又一次转化为求三角函数的最值问题.第(3)问有多种引入参数的方法,方法一:由x2+y2=S,联想到三角公式cos2α+sin2α=1,参进参数α.通过“三角换元法”将问题转化为熟悉的简单三角函数求S的最大值和最小值,还可由![]() 的有界性解不等式
的有界性解不等式![]() 求S的最大值和最小值.方法二:引进两个参数a,b,采用“对偶换元法”(和差换元)将问题转化为二次函数求解.
求S的最大值和最小值.方法二:引进两个参数a,b,采用“对偶换元法”(和差换元)将问题转化为二次函数求解.
解:(1)设![]() 则
则![]() 且sin2θ+cos2θ=k2(x2+y2)=1,则由条件得
且sin2θ+cos2θ=k2(x2+y2)=1,则由条件得![]() 即
即![]()
设![]() 则
则![]() 解得t=3或
解得t=3或![]() 或
或![]()
(2)由![]() 得
得![]()
令![]() (θ为参数).
(θ为参数).
将f(x,y)转化为g(θ)=|6cosθ-6sinθ-12|,
![]()
当![]() 即
即![]() 时,
时,![]()
当![]() 即
即![]() 时,
时,![]()
(3)解法一 设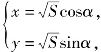 代入条件得4S-5Ssinαcosα=5,
代入条件得4S-5Ssinαcosα=5,
解得![]()
∵-1≤sin2α≤1,∴3≤8-5sin2α≤13.
![]()
解法二 设x=a+b,y=a-b,代入条件整理得3a2+13b2=5,则![]()
![]()
![]()
解法三 由S=x2+y2,设![]()
则![]() 代入已知式得
代入已知式得![]() 移项平方整理得100t2+39S2-160S+100=0,∴39S2-160S+100≤0,解得
移项平方整理得100t2+39S2-160S+100=0,∴39S2-160S+100≤0,解得![]()
![]()
例2 (1)已知定点Q(0,-4),P(6,0),动点C在椭圆![]() 上运动,求△QPC面积的最大值和最小值;
上运动,求△QPC面积的最大值和最小值;
(2)在双曲线x2-2y2=2上求一点P,使它到直线x+y=0的距离最短,并求出这个最短距离.
解题策略 第(1)问,定点Q(0,-4),P(6,0)的距离|PQ|是定值,点C是椭圆上的动点,要求△QPC面积的最值实质上是求点C到直线PQ的距离d的最值.若设C(x,y),则d的表达式必包含x,y两个变量,消元后带有无理式,不易求解;若设C(3cosθ,2sinθ),则利用三角知识易求得d的最值.第(2)问,利用双曲线的参数方程,通过求距离将所得等式转化为一元二次方程,并用判别式法求d的最小值和相应点P的坐标.
解:(1)由题意易知直线PQ的方程为![]()
又∵椭圆的参数方程为![]() (θ为参数,且0≤θ<2π),
(θ为参数,且0≤θ<2π),
则椭圆上点C(3cosθ,2sinθ)到直线PQ的距离
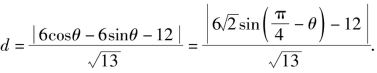
显然,当![]() 时,d最大,且
时,d最大,且![]() 此时S△PQC的最大值为
此时S△PQC的最大值为![]()
当![]() 时,d最小,且
时,d最小,且![]() 此时S△PQC的最小值为
此时S△PQC的最小值为![]()
(2)设双曲线![]() -y2=1上一点P的坐标为
-y2=1上一点P的坐标为![]() 则它到直线x+y=0的距离为
则它到直线x+y=0的距离为
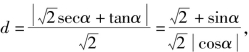 从而
从而![]() 去分母整理,得
去分母整理,得
![]()
∵sinα是实数,![]() 解之,得
解之,得![]()
当![]() 时,
时, 或
或![]()
这时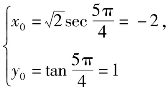 或
或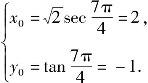

图4-2
故当双曲线上的点P为(-2,1)或(2,-1)时,它到直线x+y=0的距离最小,这个最小值为![]()
例3 (1)直线l过抛物线y2=2px(p≠0)的焦点,并且与抛物线交于A、B两点,求证,对于抛物线的任何给定的一条弦CD,直线l不是CD的垂直平分线;
(2)如图4-2所示,抛物线C1:x2=4y,C2:x2=-4y,点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
解题策略 第(1)问,引进抛物线y2=2px的参数形式:![]() (t为参数).将抛物线实行动点化处理.即设
(t为参数).将抛物线实行动点化处理.即设![]() 利用l过焦点与CD的中点M,求出直线l的斜率和直线CD的斜率.再利用反证法推出若l与CD垂直会产生矛盾,从而使问题获证.第(2)问,直接利用抛物线的参数方程表示A的坐标
利用l过焦点与CD的中点M,求出直线l的斜率和直线CD的斜率.再利用反证法推出若l与CD垂直会产生矛盾,从而使问题获证.第(2)问,直接利用抛物线的参数方程表示A的坐标![]() 的坐标
的坐标![]() 从而得到AB中点N的坐标
从而得到AB中点N的坐标![]() 在求得切线MA,MB的方程后把点M坐标(x0,y0)代入.易得双参数t1,t2是关于t的一元二次方程的根,利用韦达定理并消去参数可得所求点N的轨迹方程.
在求得切线MA,MB的方程后把点M坐标(x0,y0)代入.易得双参数t1,t2是关于t的一元二次方程的根,利用韦达定理并消去参数可得所求点N的轨迹方程.
解:(1)证明 ∵直线l与抛物线交于两点,∴l与抛物线的轴不可能重合或平行,设![]() 不可能关于抛物线的轴对称,∴t1+t2≠0,则C,D的中点坐标
不可能关于抛物线的轴对称,∴t1+t2≠0,则C,D的中点坐标![]()
∵l过焦点![]() 且过点M.(https://www.xing528.com)
且过点M.(https://www.xing528.com)
∴直线l的斜率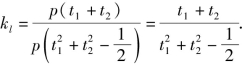
又∵直线CD的斜率![]()
若直线l垂直平分CD,则kl·kCD=-1,即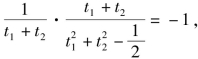
则![]() 这与
这与![]() 矛盾.
矛盾.
∴直线l不是CD的垂直平分线.
(2)当M为原点O时,A,B重合于O,中点为O,即点N的轨迹为点(0,0),当A,B不重合于O时,设点A的坐标为![]() 点B的坐标为
点B的坐标为![]() 则点N的坐标为
则点N的坐标为![]()
切线MA的方程为![]()
同理切线MB的方程为![]() 又∵点M的坐标为(x0,y0),且在AM,BM上,
又∵点M的坐标为(x0,y0),且在AM,BM上,
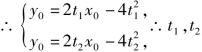 是方程4t2-2tx0+y0=0的两个根,
是方程4t2-2tx0+y0=0的两个根,
由韦达定理得![]()
∴可得![]()
即点N的轨迹方程为![]() 也满足,故点N的轨迹方程为
也满足,故点N的轨迹方程为![]()
例4 (1)过点P(2,1)作椭圆![]() 的弦,求:
的弦,求:
❶P为弦中点时,弦所在的直线方程;
❷P为弦三等分点时,弦所在的直线方程.
(2)已知椭圆![]() 的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
❶当t=4,|AM|=|AN|时,求△AMN的面积;
❷当2|AM|=|AN|时,求k的取值范围.
解题策略 第(1)问,可运用直线的参数方程,其标准式为![]() (t为参数),表示过点P0(x0,y0),倾斜角为α的直线.参数t的几何意义是:|t|表示直线上的点P(x,y)到定点P0(x0,y0)的距离,当P在P0点上方时,t>0;当P在P0点下方时,t<0;当P与P0点重合时,t=0,反之亦然.第(2)问,涉及直线过定点的旋转问题,通常用直线的参数方程解比较简捷.
(t为参数),表示过点P0(x0,y0),倾斜角为α的直线.参数t的几何意义是:|t|表示直线上的点P(x,y)到定点P0(x0,y0)的距离,当P在P0点上方时,t>0;当P在P0点下方时,t<0;当P与P0点重合时,t=0,反之亦然.第(2)问,涉及直线过定点的旋转问题,通常用直线的参数方程解比较简捷.
解:(1)设直线l的方程为![]() (t为参数),α为l的倾斜角.
(t为参数),α为l的倾斜角.
将l的方程代入x2+4y2=16得(2+tcosα)2+4(1+tsinα)2=16.
整理得(cos2α+4sin2α)t2+(4cosα+8sinα)t-8=0.
❶由定点P是弦AB的中点,![]() 即4cosα+8sinα=0.
即4cosα+8sinα=0.
![]()
∴直线l的方程为![]() 即x+2y-4=0.
即x+2y-4=0.
❷由定点P是弦AB的三等分点,∴t1=-2t2或2t1=-t2即t1+t2=-t2或t1+t2=-t1,同时,![]() 或
或![]() 则t1t2=-2(t1+t2)2.
则t1t2=-2(t1+t2)2.
即![]()
整理,得3cos2α+16sinαcosα+12sin2α=0.
即12tan2α+16tanα+3=0,解方程,得![]()
∴直线l的方程为![]()
即![]() 或
或![]()
(2)❶当t=4时,A(-2,0),设AM的倾斜角为![]()
则AM的参数方程为![]() (m为参数).由MA⊥NA,
(m为参数).由MA⊥NA,
则AN的参数方程为![]() (n为参数).
(n为参数).
又M,N在椭圆E上,则
![]()
![]()
又|AM|=|AN|.∴|m|=|n|,即![]()
则![]()
![]() 设AM的倾斜角为
设AM的倾斜角为![]()
则AM的参数方程为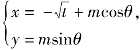 (m为参数).由MA⊥NA.
(m为参数).由MA⊥NA.
则AN的参数方程为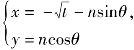 (n为参数).
(n为参数).
又M,N在椭圆E上,则![]()
![]()
又2|AM|=|AN|,∴2|m|=|n|,即![]()
![]() 即
即![]() ①
①
当k3=2时①式不成立,有![]()
即![]()
即(k2+1)(k-2)(k3-2)<0,即![]()
解得![]() 故k的取值范围为
故k的取值范围为![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




