通常解答数学问题总是习惯于把注意力集中在主变元上,思考探求参变元的取值或其范围,这种思考问题的方法当然可以,但不一定是一条好的思路,即使能解但其过程会非常烦琐.若密切注意命题的求解趋势,依从条件与结论的内在联系变换思考方向,视其参变元为主变元进行研究、推导,也能找到解决问题的途径,有时还能获得问题的妙思巧解,这就是参变分离,一种“反客为主”的方法.参变分离法就是把所求参变量与其他变量分离开来,通过研究其他变量构成的解析式的性质来确定所求参变量的范围.这一解法具有思路清晰、有章可循、易于操作等特点.
参变分离法主要用于解以下题型:
(1)函数或方程中求参数的范围问题;
(2)不等式恒成立和能成立问题中求参数的范围问题.
例1 (1)设关于x的方程k·9x-k·3x+1+6(k-5)=0在区间[0,2]内有解,求实数k的取值范围;
(2)已知方程sin4x+2asin2x-2a-2=0有解,试确定实数a的取值范围.
解题策略 如果从方程角度考虑,两小题的解答都比较复杂.第(1)问,设t=3x,原方程化为kt2-3kt+6(k-5)=0,由x∈[0,2]得t∈[1,9],则原问题转化为关于t的一元二次方程在t∈[1,9]上是否有解的问题.当然还有一解两解之分,运算量大.通过参变分离,转化为k关于t的函数求值域就方便许多.第(2)问,原方程改写为2a(sin2x-1)=2-sin4x,显然sin2x≠1,设t=sin2x,0≤t<1,则关于t的一元二次方程有解且解在[0,1)之间,也还有一解两解的问题,烦琐且易出错,实行参变分离,把方程转化为函数,运用函数的思想方法解题则很简捷.
解:(1)令t=3x,由x∈[0,2]得t∈[1,9],原方程化为kt2-3kt+6(k-5)=0,即 当
当![]() 时,k有最大值8;当t=9时,k有最小值
时,k有最大值8;当t=9时,k有最小值![]()
所以,要使原方程有解,必须有![]() 即实数k的取值范围为
即实数k的取值范围为![]()
(2)原方程可以改写成2a(sin2x-1)=2-sin4x,显然sin2x≠1.
设t=sin2x,则![]()
则![]()
易知函数f(t)在t∈[0,1)上为减函数,∴f(t)≤f(0)=-1,即a≤-1,
∴实数a的取值范围为(-10,-1].
例2 (1)若关于x的不等式(2x-1)2<ax2的解集中的整数恰有3个,则实数a的取值范围是________;
(2)关于x的不等式x2-ax+2a<0的解集中恰有两个整数,则实数a的取值范围是________;
(3)若关于x的不等式ax2-|x+1|+2a<0的解集为∅,求实数a的取值范围.
解题策略 本例三小题都是含参数不等式解集的讨论.可以有多种解法,这里重点放在参变分离法及求参数的取值范围上.第(1)问,参变分离后运用图像法解.第(2)问,运用参变分离,然后通过数形结合及考察相应函数的单调性求解.第(3)问,从反面考虑,原问题转换成“对任意x∈R,都有ax2-|x+1|+2a≥0”,再运用参变分离法转化为函数问题求解.
解:(1)依题知a>0,且x≠0.
由此,得![]()

图4-1
设![]() 如图4-1所示,当且仅当
如图4-1所示,当且仅当![]() 即
即![]() 也即
也即![]() 时,
时,![]() 的解集中有3个整数1,2,3.
的解集中有3个整数1,2,3.
∴关于x的不等式(2x-1)2<ax2的解集中有3个整数时,![]()
故实数a的取值范围是![]()
(2)原不等式可化为x2<a(x-2).
❶当x>2时,![]()
设![]() 可得f(x)在区间(2,4)内单调递减,在区间(4,+∞)内单调递增,因此,f(4)<f(5)<f(3)=f(6),于是f(5)<a≤f(3),得
可得f(x)在区间(2,4)内单调递减,在区间(4,+∞)内单调递增,因此,f(4)<f(5)<f(3)=f(6),于是f(5)<a≤f(3),得![]()
❷当x<2时,![]()
设![]() 则f(x)在区间(0,2)内单调递减,在区间(-∞,0)内单调递增,因此,f(-2)=f(1)<f(-1)<f(0),于是f(1)≤a<f(-1),得
则f(x)在区间(0,2)内单调递减,在区间(-∞,0)内单调递增,因此,f(-2)=f(1)<f(-1)<f(0),于是f(1)≤a<f(-1),得![]() 综上,a的取值范围是
综上,a的取值范围是![]()
(3)由题意,对任意x∈R,都有ax2-|x+1|+2a≥0,即![]() 对任意x∈R成立.
对任意x∈R成立.
设![]() 则
则![]() 对任意x∈R恒成立⟺a≥f(x)max.
对任意x∈R恒成立⟺a≥f(x)max.
令t=x+1,则![]()
❶当t=0时,g(t)=0;
❷当t>0时, 当且仅当
当且仅当![]() 时,g(t)有最大值
时,g(t)有最大值![]()
❸当t<0时, 当且仅当
当且仅当![]() 时,g(t)有最大值
时,g(t)有最大值![]()
综上得,f(x)=g(t)有最大值![]() 故a的取值范围是
故a的取值范围是![]()
例3 (1)设函数![]() 其中a∈R,n是任意给定的自然数,且n≥2,若当x∈(-∞,1]时,f(x)有意义,求a的取值范围;
其中a∈R,n是任意给定的自然数,且n≥2,若当x∈(-∞,1]时,f(x)有意义,求a的取值范围;
(2)已知函数p(x)=x3+(k-1)x2+(k+5)x-1(其中k∈R)在区间(0,3)上不单调,求k的取值范围.
解题策略 第(1)问,若能把参变元a与变元n,x分离开来,则问题变得相当明朗,解题的方向也就确定了;第(2)问,三次函数在区间上不单调即其导函数对应的方程在区间上有实根且无重根,通过对p′(x)=0实行参变分离将本题转化为求函数的值域.
解:(1)由题意有1+2x+…+(n-1)x+nxa>0对x∈(-∞,1]且n≥2恒成立,
即![]() 恒成立.(https://www.xing528.com)
恒成立.(https://www.xing528.com)
于是原题变为求![]() 在n≥2,x∈(-∞,1]时的最大值.
在n≥2,x∈(-∞,1]时的最大值.
因为n≥2,而![]() 是x∈(-∞,1]上的递减函数,
是x∈(-∞,1]上的递减函数,
即g(x)在x∈(-∞,1]上是递增函数;当x=1时,![]()
故![]()
(2)p′(x)=3x2+2(k-1)x+k+5,因为p(x)在区间(0,3)上不单调,
所以p′(x)=0在(0,3)上有实数解且无重根,
由p′(x)=0得k(2x+1)=-(3x2-2x+5),当2x+1≠0时有
![]()
令t=2x+1,有t∈(1,7),记![]() 则h(t)在(1,3)上单调递减,在(3,7)上单调递增,所以有h(t)∈[6,10),
则h(t)在(1,3)上单调递减,在(3,7)上单调递增,所以有h(t)∈[6,10),
于是![]() 得k∈(-5,-2].
得k∈(-5,-2].
而当k=-2时,p′(x)=0在(0,3)上有两个相等的实根x=1,故舍去,所以k∈(-5,-2).
例4 (1)对于![]() 恒成立,求实数m的范围;
恒成立,求实数m的范围;
(2)求实数a的取值范围,使得对任意实数x和任意![]() 恒有
恒有![]()
解题策略 第(1)问,二次不等式在某区间上恒成立,一般有两种解题途径:一是构造二次函数,借助数形结合,得到确定图像位置的不等式或不等式组;二是通过参变分离转化为求三角函数的最值,为使解题过程简捷,都可结合换元法求解,比较两种解法,参变分离的优势比较明显.第(2)问,从形式上看就比较复杂,一是多参数,a与θ都是参数,要考虑分层求解,二是平方和,这种结构与两点间的距离公式相似,故可从这一角度寻找解题思路破题,换元法与参变分离法在解题中起重要作用.
解:(1)解法一 原不等式变形为:-sin2θ+2msinθ-2m-1<0,
即sin2θ-2msinθ+2m+1>0,
令sinθ=t,t∈[0,1],∴t2-2mt+2m+1>0,令f(t)=t2-2mt+2m+1,
∴原题转化为f(t)>0在t∈[0,1]上恒成立.
 或
或
或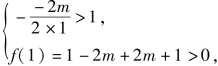
解得:![]() 或0≤m≤1或
或0≤m≤1或![]()
即m的取值范围为![]()
解法二 原不等式变形为m(2sinθ-2)<2-cos2θ.
当![]() 时,不等式恒成立.
时,不等式恒成立.
当![]() 时,
时,![]() 即
即![]()
令1-sinθ=t,则sinθ=1-t,0<t≤1,则![]()
![]() 在t∈(0,1]上单调递减.
在t∈(0,1]上单调递减.
![]()
(2)令y=x,则原不等式等价于

则原不等式的几何意义是求点Q(x,y)与点P(-3-2sinθcosθ,-asinθ-acosθ)的距离的平方大于或等于![]()
换一个角度看,点P(-3-2sinθcosθ,-asinθ-acosθ)到直线x-y=0的距离的平方大于或等于![]() 即
即

即![]() 此时实现了对x∈R原不等式恒成立,从而消去了x,留下含有θ和a的不等式.
此时实现了对x∈R原不等式恒成立,从而消去了x,留下含有θ和a的不等式.
下面解决的是对任意![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
参变分离得 或
或
令![]() 则
则![]()
![]()

或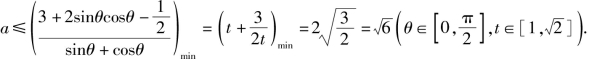
综上所述,![]() 或
或![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




