变元四大策略：均值代换、和差代换、倒置代换、常值代换

换元法解题运用比较多的除了整体代换、局部代换、对称代换外尚有一些技巧性较强的变元策略，它们依次是均值代换、和差代换、倒置代换、常值代换.

均值代换中的均值是指n个变量的算术平均数，当其为定值时可运用“算术—几何平均不等式”即基本不等式直接予以解答或证明.

如果题设有x+y=2k(常数)的形式，则可引入参数t，分别用k+t，k-t代换x和y，用和差代换解决某些数学问题，简洁明快.

根据题设中数或式的结构特征，利用倒置变换的方法，轻松实现难以入手问题的转换，化难为易，方法灵活.

常值代换是指变换题中已知数与未知数的角色，将“已知”暂时化为“未知”，“未知”又暂时看作“已知”，以此入手解题，非常巧妙，独树一帜.

例1　(1)设a，b，c均为非负实数，求证:

(2)设x，y为正数，x+y=1，证明：

解题策略　运用基本不等式证明不等式有时会出现“放缩过头”的状况,而使证明陷入僵局，第(1)问，如用a2+b2≥2ab，则有同理于是有而实际上，可得两者矛盾，说明上述用a2+b2≥2ab来缩小a2+b2有点过头,所以用均值代换应当把握好放缩的尺度，注意“适度”.第(2)问，对于x+y=1这样的条件，除了想到一般的基本不等式外，还应注意“1”的妙用.乘以“1”或除以“1”，表达式的值均不变，这样往往可以把原表达式表示成更有明显特征的表达式，有利于证明过程的实施.

证明　(1)由a2+b2≥2ab得2(a2+b2)≥(a+b)2，即

也即同理可得

所以

(2)又

由题意，得当且仅当时等式成立.

当且仅当时取“=”,

所以

例2　(1)设x1，x2是方程x2-6x+1=0的两个根，求证：对一切自然数都是偶数；

(2)在△ABC中，a,b,c分别是角A，B，C的对边，设求sinB的值；

(3)已知p，q，r≥0,p+q+r=1.证明：7(pq+qr+rp)≤2+9pqr.

解题策略　本例各题用和差代换证明或求解，可起到“降元”的作用，从而变繁为简，化难为易.

解：(1)证明　由方程根与系数关系，x1+x2=6,x1x2=1.

故令x1=3+t，x2=3-t，由x1x2=1得(3+t)(3-t)=1.∴t2=8.

因此都是偶数.

(2)可设即

∴B=π-(A+C)=π-2θ,sinB=sin2θ,

由a+c=2b可得

故

则

因此(www.xing528.com)

(3)证明　设则a+b+c=0.

原不等式等价于4(ab+bc+ac)≤9abc.

根据a，b，c的对称性，不妨设a≥b≥c,∴c≤0,a+b≥0,c=-(a+b).

∴4(ab+bc+ac)=-4(a2+b2+ab),9abc=-9ab(a+b).

故原不等式⟺4(a2+b2+ab)≥9ab(a+b).

当ab≤0时，原不等式⟺4[(a+b)2-ab]≤9ab(a+b),显然成立；

当ab>0时,原不等式⟺4[(a+b)2-ab]≤9ab(a+b).

显然成立，

∴4(a2+b2+ab)≥-3ab≥-9ab(a+b)=9abc.

综上，原不等式得证.

例3　已知数列{an}，若对n∈N*,都有an>0且

试证：

解题策略　本例是数列不等式的证明，直接证明难以入手，用数学归纳法涉及放缩法也非易事，若把条件变形为再取倒数得研究倒数数列的特点可开辟一条证题的新路，事实上，当我们遇到数列{an}有某种性质难以入手时，转化为先研究的性质往往可以达到解题目的.

证明　∵an>0且则得0<an<1.

即则

以上各式相加，得：

例4　(1)设x，y都是正数,且x+y=1，证明：

(2)解方程：

解题策略　本例两小题采用常值代换.第(1)问，将所证不等式左边分子上的“1”用x+y代换，立即可采用基本不等式证明;第(2)问，直接解无理方程运算量大.若把方程变形为然后化常量5为变量y2.读者看一看将会出现怎样的情况？

解：(1)证明　∵x+y=1,

当且仅当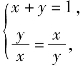即时取“=”.∴原不等式得证.

(2)原方程化为　　①

令5=y2,则①式为　　②

设

则②式即为　|PF1|+|PF2|=20.

即动点P(x,y)到两定点的距离之和等于20，且可见动点P的轨迹是椭圆.其标准方程为

经检验知，它们都是原方程的根.