变量代换是借助于引入新变量来实现问题转化的一种解题策略,新变量的引入没有固定的形式,它依赖问题本身的结构和特点,许多代数题目都可以根据题目的特点,应用三角函数进行适当的代换,结合三角恒等式,将代数问题转化为三角问题,使问题得以简捷地获解,当然,用三角函数或三角函数式代换代数式中的变量时应由旧变量的取值范围确定新元的取值范围.推而广之,将某一个系统中的问题对应地转化到另一个系统中去解决,这是变量代换最本质的作用.
三角换元主要用来解决如下结构的数学问题:
(1)f2(x)+g2(x)=R2型:可设f(x)=Rcosθ,g(x)=Rsinθ去求解.对θ的取值范围作相应限定,下同.
(2)![]() 与|x|≤a型:可设x=acosθ或x=asinθ去解.
与|x|≤a型:可设x=acosθ或x=asinθ去解.
(3)f2(x)-g2(x)=R2型:可设f(x)=Rsecθ,g(x)=Rtanθ去解.
(4)![]() 型:可设f(x)=Rtanθ去解.
型:可设f(x)=Rtanθ去解.
(5)![]() 或|x|≥R型:可设x=Rsecθ或x=Rcscθ去解.
或|x|≥R型:可设x=Rsecθ或x=Rcscθ去解.
(6)![]() 型:可设
型:可设![]() 运用万能置换公式去解.
运用万能置换公式去解.
(7)![]() 型:可设x=tanα,y=tanβ,运用两角和或差的正切公式去解.
型:可设x=tanα,y=tanβ,运用两角和或差的正切公式去解.
由函数式隐含的几何意义,通过三角换元转化为运用数形结合法去解,如有些问题可在三角换元后转化为直线与二次曲线的关系问题.
例1 (1)求函数![]() 的最大值和最小值;
的最大值和最小值;
(2)求函数![]() 的值域;
的值域;
(3)求函数![]() 的值域;
的值域;
(4)已知1≤x2+y2≤2,求z=x2-xy+y2的最值.
解题策略 无理函数的最值或值域的求法是一个难点,难在如何才能去掉根号使之成为有理函数,而三角换元借助于三角公式能实现这一转化,问题在于所给出的函数解析式常常并非一目了然地能找到三角换元的途径, 需要对解析式中的被开方式实施变形,找准方向,实现三角换元.对于第(1)问中含有两个无理式,则必须找到两个无理式中被开方式的关联,一步到位实现化无理为有理、化一般代数式为三角式的目标,第(4)问是二元函数,关键在于如何由条件1≤x2+y2≤2,实施三角换元,且要总体考虑,当然三角换元必须由条件对角的范围进行限定.在这一限定下运用三角知识,求解三角换元可使较复杂的问题简单化.
解:(1)由于4≤x≤5,故可令![]()
则原式变为![]()
当![]() 即
即![]() 时,y取得最大值2;
时,y取得最大值2;
当![]() 即x=5时,y取得最小值1.
即x=5时,y取得最小值1.
(2)函数的定义域为R,令![]()
则![]()
由于![]()
而当![]() 时,y为减函数,此时-2<y<-1,
时,y为减函数,此时-2<y<-1,
当![]() 时,y为增函数,此时-2≤y<1.
时,y为增函数,此时-2≤y<1.
故函数的值域为[-2,1).
(3)解法一 ∵2x2-4x+6=2(x-1)2+4,∴可设![]()
则![]()
设![]() 则u>0,从而
则u>0,从而![]()
![]() 且u>0,∴u≥1,
且u>0,∴u≥1,
![]() 故函数的值域为
故函数的值域为![]()
解法二 由解法一得![]() 则u为
则u为![]() 与点
与点![]() 连线的斜率.
连线的斜率.
设过点A的直线方程为![]() 即
即![]() 显然k>0,当直线与半圆x2+y2=1(0<x≤1,-1<y<1)相切时,
显然k>0,当直线与半圆x2+y2=1(0<x≤1,-1<y<1)相切时,![]() 解得k=1,数形结合易得k≥1,即u≥1.
解得k=1,数形结合易得k≥1,即u≥1.![]() 故函数的值域为
故函数的值域为![]()
(4)令x=kcosθ,y=ksinθ,则1≤k2≤2.
又![]()
当k2=2,sin2θ=-1时,zmax=3;
当k2=1,sin2θ=1时,![]()
例2 (1)已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是________;
(2)对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0,且使|2a+b|最大时,![]() 的最小值为________.
的最小值为________.
解题策略 第(1)问,由于条件是三元等式,如何实现三角换元需要精心构思,可以有多种三角换元的方法;第(2)问,若将4a2-2ab+4b2-c=0变形为![]() 联想到三角公式sin2α+cos2α=1,可令
联想到三角公式sin2α+cos2α=1,可令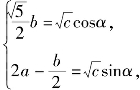 从而把求|2a+b|的最大值转化为三角函数求最大值.从而说明了数学是灵动的,通过思维完成构想,一旦成功何等快意,正如欧阳修的诗句:“一阕声长听不尽,轻舟短楫去如飞.”
从而把求|2a+b|的最大值转化为三角函数求最大值.从而说明了数学是灵动的,通过思维完成构想,一旦成功何等快意,正如欧阳修的诗句:“一阕声长听不尽,轻舟短楫去如飞.”
解:(1)解法一 将c=-(a+b)代入a2+b2+c2=1得![]()
整理得![]() 令
令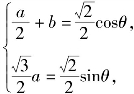 则
则![]()
∴a的最大值为![]()
解法二 将c=-(a+b)代入a2+b2+c2=1得![]()
令a=x+y,b=x-y,代入上式得6x2+2y2=1.由椭圆的参数方程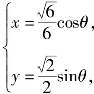
则![]()
∴a的最大值为![]()
解法三 由a2+b2+c2=1得b2+c2=1-a2.(https://www.xing528.com)
令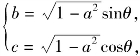 代入a+b+c=0得
代入a+b+c=0得![]()
当![]() 时,得
时,得![]()
即 解得
解得![]() 即
即![]()
∴a的最大值为![]()
(2)由4a2-2ab+4b2-c=0得![]() 令
令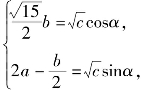
则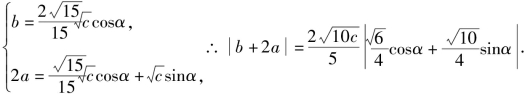
当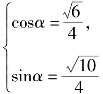 时
时![]()
此时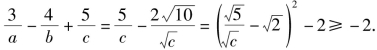
![]() 的最小值为-2.
的最小值为-2.
例3 (1)给定数列{an},且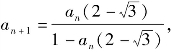 求a2020-a1460;
求a2020-a1460;
(2)数列{an}、{bn}(n∈N)满足: 求证:对任意的n∈N恒有2n+2an<π<2n+2bn.
求证:对任意的n∈N恒有2n+2an<π<2n+2bn.
解题策略 本例两小题是递推数列求通项或证明与通项相关的数列不等式,此处我们尝试用三角换元的方法求解或证明.第(1)问,由递推式的结构特点,可构造两角和的正切公式求解.第(2)问,涉及两个递推数列且所给递推式又都是无理式,若能通过巧妙的三角换元并借助当![]() 时,有sinx<x<tanx可得到极其简捷的证法.三角换元的妙用常常可以达到神奇的解题效果.
时,有sinx<x<tanx可得到极其简捷的证法.三角换元的妙用常常可以达到神奇的解题效果.
解:(1)由递推式的结构特点,可构造三角公式求解.
![]() 令an=tanαn.
令an=tanαn.
则![]()
an+2=tan(αn+15°+15°),…,an+12=tan(αn+180°)=tanαn=an,
而2020=1460+50×12,∴a2020-a1460=0.
(2)证明 仔细观察数列{an}、{bn}的递推关系式可以发现:0<an<1,bn>0.
由此令![]() 则有
则有![]()
从而构造三角函数得到![]()
![]() 数列{αn}是首项为
数列{αn}是首项为![]() 公比为
公比为![]() 的等比数列
的等比数列![]()
同理可得![]()
利用熟悉的不等式:![]() 则sinx<x<tanx.此处
则sinx<x<tanx.此处![]()
则有![]()
例4 (1)已知a>0,b>0且a+2b=1,求证:![]()
(2)a,b,x,y均为正数,且![]() 求证:
求证:![]()
(3)求证:![]()
(4)设a,b,c是正实数,且abc+a+c=b,求证:![]()
解题策略 代数问题三角化,可以充分利用三角函数的特有性质,使较为复杂的不等式的证明问题得以简化,但要注意角的范围和三角函数的有界性.第(1)问,通过三角换元,弦化切,运用基本不等式证明;第(2)问,即使是三角换元也可以有多种证法,可以通过这些方法锻炼发散思维能力,力求对突破难点有所禆益;第(3)问,所证不等式即为求函数![]() 的值域是否为
的值域是否为![]() 但是在运用三角换元时由于形式上不是很明朗,故必须先对被开方式进行适当变形,找到如何实施三角换元化无理为有理的途径;第(4)问,由abc+a+c=b得
但是在运用三角换元时由于形式上不是很明朗,故必须先对被开方式进行适当变形,找到如何实施三角换元化无理为有理的途径;第(4)问,由abc+a+c=b得![]() 其特征与两角和的正切公式
其特征与两角和的正切公式![]() 相似,证明思路顿时凸现!
相似,证明思路顿时凸现!
(1)证明 由a>0,b>0,a+2b=1,设![]()
则有: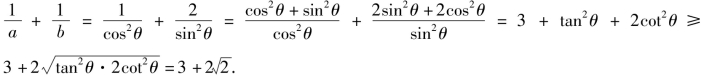
当且仅当tan2θ=2cot2θ,即tan4θ=2.也就是![]() 从而
从而![]() 时取得等号.
时取得等号.
(2)证法一 依题设![]()
即![]()
证法二 由证法一题设可得:a=xsin2θ,b=ycos2θ.
![]() 故原不等式得证.
故原不等式得证.
证法三 由证法一题设可得:![]()
(3)∵3-2x-x2=4-(x+1)2≥0,∴|x+1|≤2,设![]()
则![]()
又由![]() 得
得![]()
从而![]()
故![]()
(4)设![]()
由abc+a+c=b得![]()
=cos2α+cos2β-2cos2(α+β)+2
=2cos(α+β)cos(α-β)-2cos2(α+β)+2
≤2cos(α+β)-2cos2(α+β)+2
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




