巧用辅助元法解数学题

在解题过程中，通过引入一个或几个新变量来代替原式中某些量或式以实现变量替换，从而使问题得以解决，这种解题方法叫作换元法，又称辅助元法.辅助元法的理论根据是等量代换.

辅助元法可以把分散的条件联系起来，或者把隐含的条件显示出来，或者把条件与结论联系起来，或者变换为熟悉的形式，把繁难的计算和推理论证简化，从而达到化难为易，化繁为简、化未知为已知的目的，有利于问题的解决.换元中一定要注意新元的约束条件和整体置换策略的运用，适时补充条件以符合原未知数取值范围的要求.

辅助元法的基本步骤如下：

(1)把原问题中某个式子或某几个式子分别看成一个整体；

(2)引入新元代替这些式子，使以新元为基础的问题较为简洁易解；

(3)对以新元为基础的问题进行解答，得出结果；

(4)再代回原来的式子中求出原变量的结果.

合理运用辅助元法解题策略，可以使解题能力更上一个台阶.

例1　(1)解方程：

(2)解方程：

(3)解方程：

解题策略　通过换元化无理为有理，思考的方法是对的，但上述方程中无理式不止一个，关键要认清这些无理式之间的关系，即通过运算或变形有可能得到什么结果，第(1)问可采用平均代换，第(2)(3)问可引进两个新元，寻求两个新元之间的联系.

解：(1)令则由上述两式平方之差，有x-5=2xt,即

于是即

从而即x2-x-5=0,解得

经检验，是原方程的根.

(2)设于是有方程组：

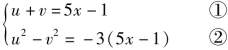　当5x-1≠0时，②÷①得：u-v=-3　　③

由①和③解得：

解这个方程得：

当5x-1=0时，适合原方程.

∴原方程的解是

(3)注意到三次根式和的立方和为常数.

故可设则u3+v3=35.

又由原方程得u2+v2=uv+7,即u2-uv+v2=7.

从而

于是u、v是方程y2-5y+6=0的两个根，解得y1=2,y2=3.

当u=2,v=3时，x1=0；当u=3,v=2时，x2=-19.

经检验，x1=0,x2=-19都适合原方程.∴原方程的解是x1=0,x2=-19.

例2　(1)解方程2×49x2-9×14x2+7×4x2=0;

(2)已知函数且x≠0)，若实数a,b使得f(x)=0有实根，求a2+b2的最小值；

(3)方程ax2-4ax+1=0(a≠0)的两个正数解m，n满足|lgm-lgn|≤1.求a的取值范围.

解题策略　第(1)问是解指数方程，由于底数不相同，无法化为同底，故需设两个新元，再通过分解因式得两个新元之间的关系再解之.第(2)问，函数解析式中含有和令通过局部换元、整体处理使原问题转化为关于t的二次函数.又由于t有范围限制，可采用变更主元，即以a，b为主元，得到直线方程，转化为点到直线的距离问题，解题中出现t2+1的形式，又一次局部换元(中途换元在变形过程中才能发现)，在多次换元过程中，新元的范围确定非常重要.第(3)问，方程ax2-4ax+1=0(a≠0)有正根m，n.用韦达定理使m+n，mn用a表示.将超越式|lgm-lgn|≤1变更为关于m+n，mn的代数不等式，并把m+n，mn用a表示的式子代入，即可得关于a的不等式，即可求出a的取值范围，整体代换在解题过程中发挥重要作用.

解：(1)原方程变形为2×(7x2)2-9×(7x2)×(2x2)+7×(2x2)2=0.

设y=7x2,z=2x2,则有2y2-9yz+7z2=0.

分解方程左边，则有(y-z)(2y-7z)=0.

所以y=z或2y=7z.即7x2=2x2或2×7x2=7×2x2.

由7x2=2x2,可得

由2×7x2=7×2x2,可得

经检验，x=0,x=±1均为原方程的根.

(2)由可得令则原问题转化为方程t2+at+b-2=0根的讨论.

若将a,b视作主元，t为参数，则方程变为ta+b+t2-2=0,P(a,b)为直线l：ta+b+t2-2=0上一点，则=a2+b2.

设原点到直线l的距离为d.则再令u=t2+1,则

由于在[5,+∞)上单调递增，故当u=5时函数取最小值即a2+b2的最小值为

(3)因为x∈R,a≠0,所以Δ=16a2-4a≥0，故a<0或(www.xing528.com)

由韦达定理得从而可得　　①

又由已知|lgm-lgn|≤1，得-1≤lgm-lgn≤1，即lgn-1≤lgm≤1+lgn，从而，有故所以即

由此可得

又因为所以　　②

由①②得a的取值范围为

例3　(1)解不等式

(2)解不等式

(3)已知a>b>0,θ为锐角，求证：

解题策略　本例第(1)(2)两问是解无理不等式，一般将其转化为有理不等式组.若运用换元法，即抓住无理式结构，用一个变量进行代换，则立即转化为有理不等式，得之就不难了，当然在解答时，对于新元的取值范围应予以重视.第(3)问是三角不等式证明.

可采用整体换换元.即令k=asecθ-btanθ，通过寻找问题中隐含的几何意义转化为解析几何知识证明是个“好念头.”

解：(1)令则于是，原不等式可化为

即t2-2t-3<0，解得-1<t<3,且t≥0,即

由此解得原不等式解集为

(2)令则x2-x=t2+1(t≥0).于是原不等式可化为t2+t-2<0.

解得-2<t<1，且t≥0,即变形为

解得或

由此解得原不等式的解集为

(3)证明　令

则k可看成是过A(0,a)，B(-cosθ,bsinθ)两点的直线的斜率.

而动点B的轨迹方程为

∴当直线AB与曲线相切时，k有最小值，设过定点A且与椭圆相切的直线方程为y=k′x+a,代入椭圆方程,得(k′2+b2)x2+2k′ax+a2-b2=0.

令Δ=0，得k′2=a2-b2,　∵a>b>0且k′>0,　∴a2-b2>0,

于是

例4　(1)求函数的最小值；

(2)设a>0，求f(x)=2a(sinx+cosx)-sinxcosx-2a2的最大值和最小值；

(3)已知0<α<π，证明并讨论α为何值时等号成立.

解题策略　第(1)问，若用代数方程求解肯定较烦琐，观察本题结构，联想到与分别是复数z1=x+3i与z2=(4-x)+i的模，代入|z1|+|z2|≥|z1+z2|即可求解.第(2)问，通过换元转化为二次函数区间最值问题.第(3)问，可通过初等函数的代换，将三角不等式的证明转化为代数不等式的证明，关键是寻找合适的代换，而万能置换正合适.

解：(1)设z1=x+3i,z2=(4-x)+i,则

又因为|z1|+|z2|≥|z1+z2|,所以

当且仅当z1=kz2(k>0)时取等号，此时k=3,即x=3(4-x),x=3.

故的最小值是

(2)设sinx+cosx=t,则

时取最小值：

当时，时取最大值：

当时，t=2a时取最大值：

∴f(x)的最小值为最大值为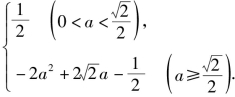

(3)证明　令则由知t>0,

由万能公式，原不等式可化为

用t(1+t2)2乘上面不等式两端，问题变为证明8t2(1-t2)≤(1+t2)2,

展开化简，得-9t4+6t2-1≤0，即-(3t2-1)2≤0.

由于以上每步可逆，故原不等式成立.

等号当且仅当即即时成立.

故当时，原不等式中等号成立.