运用函数与方程思想解立体几何问题的优化方法

在立体几何学习中，有些数学问题直接解比较困难，特别是碰到几何体中有变角或变动的线段时，此时可根据题意列出沟通已知量与变量之间的关系，通过函数与方程思想来处理.立体几何中由于动点的变化引起的最值，通常建立关于与动点相关的角度的目标函数，转化为函数最值问题求解，若在空间图形中建立空间直角坐标系，利用向量坐标法，结合条件得到方程(组)，则可用解方程组求出结果，利用函数与方程的思想方法还可以解空间图形中涉及线面关系、面面关系的探究性问题.

图3-10

例1　(2017年高考数学全国卷Ⅰ理科第16题)如图3-10所示，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O，D，E，F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形，沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得点D，E，F重合，得到三棱锥，当△ABC的边长变化时，所得三棱锥体积的最大值为________cm3.

解题策略　本题为平面图形折叠成空间图形，当折叠终止时，几何体是一个正三棱锥，这个正三棱锥底面边长是一个变元，从而导致三棱锥体积的变化，特别要提醒的是，在折叠问题中，必须注意到折叠过程中哪些要素在变化，哪些要素始终保持不变，其中不变要素是核心要素.根据平面图形的性质，寻找不变的数量关系以及直线与直线平行或垂直的位置关系，是解决折叠问题的突破口，因此折叠问题要在变图、想图、构图、用图的过程中积极思考，体会解题程序方向性，直击问题的本质，折叠问题既要看清平面转化为空间的过程，又要明确三维空间图形问题的平面化处理，这是解答立体几何问题的最常见的方法，两者是互逆的，在建立体积表达式的函数模型之后，结合函数思想求最值，通常用导数法，也可考虑运用基本不等式的方法.

解法一　由题意可知，折起后所得三棱锥为正三棱锥，当△ABC的边长变化时，设△ABC的边长为a(a>0)，则△ABC的面积为

△DBC的高为则正三棱锥的高为

∴所得三棱锥的体积

令则由t′=0，得

此时所得三棱锥的体积最大，为

图3-11

解法二　如图3-11所示，联结OD交BC于点G，

由题意知，OD⊥BC，易得

∴OG的长度与BC的长度成正比.

设OG=x，则

则所得三棱锥的体积令

则f′(x)=100x3-50x4，令f′(x)>0，即x4-2x3<0，解得0<x<2.

则当时，

∴所求三棱锥的体积最大值为

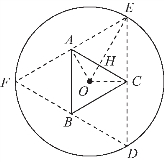
图3-12

解法三　如图3-12所示，联结OE交AC于H，联结AO，OC，设OH=x，则三棱锥的高为

三棱锥的体积V=

图3-13

当且仅当x=10-4x，即x=2时取等号，

∴所求三棱锥的体积最大值为

例2　如图3-13所示，在△ABC中，AB=BC=2，∠ABC=120°，若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是________.

解题策略　建立四面体PBCD的体积V关于PD=DA=x的函数关系式，运用函数思想方法求最值.

解法一　由AB=BC=2，∠ABC=120°，可得

要求四面体PBCD的体积，关键是寻找底面三角形BCD的面积S△BCD和点P到平面BCD的距离h，易知h≤2.设AD=x，则其中且h≤x，

∴

当且仅当即时取等号，故四面体PBCD的体积的最大值是

解法二　设PD=AD=x.∵PB=BA，△PBD≌△ABD，

为三棱锥P-BCD的高).

当平面PBD⊥平面BDC时，使四面体PBCD的体积较大.

作PH⊥BD，垂足为H、PH⊥平面BCD，h=PH=PD·sin∠PDB=x·sin∠ADB.

此时，

当且仅当时等号成立，此时

当∠ADB=90°即AD⊥BD时，VP-BCD最大值为

解法三　为三棱锥P-BCD的高).

在△ABC中，AB=BC=2，∠ABC=120°，则

设则(www.xing528.com)

在△ABD中，由余弦定理，有BD2=AD2+AB2-2AD·AB·cos∠BAC，

代值整理得在△PBD中，由余弦定理得

代值整理得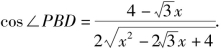

要使得VP-BCD体积最大，平面PBD需垂直于平面ABC.

过P作PM⊥BD，垂足为M，则PM为四面体P-BCD的高.

故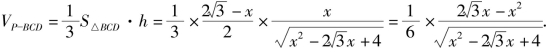

令

在t∈[1，2)上单调递减，

图3-14

∴当t=1，即时，四面体P-BCD的体积最大，为

例3　如图3-14所示，在四棱锥P-ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，

(1)求平面PAB与平面PCD所成二面角的余弦值；

(2)点Q是线段BP上的动点，当直线CQ与DP所成角最小时，求线段BQ的长.

解题策略　立体几何中由于动点的变化引起的最值问题，通常应建立关于角度的目标函数，转化为函数最值问题求解.自变量应与动点的位置有关系，在解题过程中，函数与方程的思想方法起关键作用，而空间直角坐标系的建立为利用向量坐标法、方程(组)的产生、函数式的构想创造了便利.

图3-15

解：以为x轴、y轴、z轴的正半轴建立空间直角坐标系A-xyz，如图3-15所示，则各点的坐标为B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).

(1)由题意知AD⊥平面是平面PAB的一个法向量，

设平面PCD的法向量为

则即令y=1,

解得z=1,x=1.

是平面PCD的一个法向量，从而

∴平面PAB与平面PCD所成二面角的余弦值为

(2)设

又则又

从而设1+2λ=t,t∈[1,3].

则

当且仅当即时,的最大值为

∵y=cosx在上是减函数，∴此时直线CQ与DP所成角取得最小值，

又

例4　正四棱锥S-ABCD侧棱长为l，相邻侧面的二面角多大时，其体积最大？

解题策略　若设相邻侧面的二面角为α,则可用割补法将正四棱锥的体积表示为α的函数，运用函数与方程的思想方法求体积的最大值并确定此时相邻侧面二面角的大小，本题的关键之处是建立正四棱锥S-ABCD的体积与二面角α之间的关系并归纳为如何求此函数的最大值.

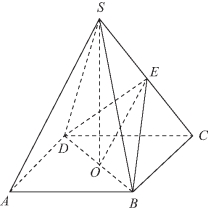
图3-16

解：如图3-16所示，作BE⊥SC,联结DE，易证△BEC≌△DEC,可得DE⊥SC.则∠BED即为相邻二面角的平面角，记为α,而三棱锥S-BCD是正四棱锥S-ABCD的一半,故问题转化为当三棱锥S-BCD的体积V最大时求α的值.

∵SC⊥BE,SC⊥DE,BE∩DE=E.∴SC⊥平面BDE.

∴借用平面BDE把三棱锥S-BDC分割成两个都以△BDE为底面的小三棱锥S-BDE和C-BDE，由于每一个小三棱锥的体积都是α的函数，则分割后的两个小三棱锥体积之和等于三棱锥S-BDC体积V这个关系，便可建立起V与α的关系，即

其中S△BDE可以用l与α表示：

即

当且仅当即α=120°时“=”号成立.

故当相邻两侧面的二面角为120°时棱锥体积最大.