运用函数与方程思想解三角问题的优化方案

函数与方程的思想方法在解三角问题中的体现主要表现在三角式的求值问题，解斜三角形以及三角函数图像及其性质的研究中，特别是求三角函数最值这类题型常常需要把函数的性质与解方程(组)思想结合起来运用.

例1　若则tanα=(　　).

解题策略　在三角求值问题中，运用方程(组)的思想是一种常见的解题策略.本例最为直接的解法是借助公式sin2α+cos2α=1结合条件，解方程组求得sinα，cosα的值，进而求tanα的值；但是若把条件平方，化为sinα，cosα的齐次式(利用1=sin2α+cos2α进行替换)分子分母同除以cos2α得关于tanα的一个方程，通过解方程得所求结果，第三种思考方法是因为而条件是故可以构造三角方程cos(α-φ)=-1(其中tanφ=2)，则易求得α的值进而求tanα的值；更为巧妙的是分析题设其结构符合等差中项a+c=2b的形式，则可构造等差数列解题.构造法思想在本题中可得到充分展示.

解法一　解方程组得故选B.

解法二　设tanα=t,则sinα=tcosα,代入得

解之得t=2,∴tanα=2,故选B.

解法三　将两边平方得cos2α+4sinαcosα+4sin2α=5.

则

化简得(tanα-2)2=0.∴tanα=2.故选B.

解法四　

∴cos(α-φ)=-1(其中tanφ=2)，则α-φ=π+2kπ(k∈Z).

即α=φ+π+2kπ(k∈Z).∴tanα=tan(φ+π+2kπ)=tanφ=2.故选B.

解法五　由于符合等差数列等差中项a+c=2b的形式，故可将原式变形为

则设

得解得

故选B.

例2　已知9sinα-3cosβ-tanγ=0　　①

cos2β+4sinαtanγ=0　　②

求证：9sinα+tanγ=0.

解题策略　这是一道条件等式的证明题，条件中有角β的三角函数，而结论中没有，消去β是必由之路，但接下来的三角恒等变形相当复杂，若仔细观察条件等式，巧妙地构造方程，可得到如下的新颖证法.当然读者可以试用常规方法证明此题，并作比较，体会构造方程、利用方程思想解题的妙处.

证法一　已知条件可变为9sinα+(-tanγ)=3cosβ

视9sinα与-tanγ为方程的两根,

问题转化为证明此方程的两根之差为零.

由于

因此，9sinα+tanγ=0.

证法二　注意到已知条件中的数学关系9=32，则①式就是以3为元的一元二次方程，而②式的左端恰为该方程的判别式，从而可得x=3.

则①式变为x2sinα-xcosβ-tanγ=0　　③

当sinα=0时，由已知条件可得tanγ=0，从而9sinα+tanγ=0；

当sinα≠0时，由②式知方程③有两个相等的实数根，

即cosβ=6sinα，代入①式得9sinα+tanγ=0.

例3　已知函数f(x)=cos2x+asinx+b(a<0).

(1)若当x∈R时，f(x)的最大值为最小值为-2,求实数a，b的值；

(2)若a=-2,b=1,设函数g(x)=msinx+2m,且当时，f(x)>g(x)恒成立，求实数m的取值范围.(www.xing528.com)

解题策略　第(1)问，f(x)为关于sinx的二次函数形式，配方后结合正弦函数的有界性以及对称轴的变动进行分类讨论进而解方程组求a，b之值；第(2)问，可以通过参变分离结合“耐克”函数性质求m的取值范围，也可以通过二次不等式在区间上恒成立问题转化为相应二次函数在区间上图像的讨论，两种解法都体现了函数思想且各具特色.

解：(1)

∴当时，

解得a=-1或a=9(舍去).∴a=-1,b=0.

当时，解得a=(舍去),即无解.

综上所述，a=-1,b=0.

(2)解法一　f(x)=-2sin2x-2sinx+2.

当时，-2sin2x-2sinx+2>m(sinx+2)恒成立，

令u=sinx+2,则

即

∴m的取值范围是

解法二　f(x)=-2sin2x-2sinx+2.

当时，-2sin2x-2sinx+2>m(sinx+2)恒成立，

令t=sinx，则h(t)=2t2+2t+mt+2m-2，则h(t)<0在上恒成立.

则即的取值范围是

例4　已知两个不共线的向量的夹角为θ，且为正实数.

(1)若与垂直，求tanθ；

(2)若求的最小值及对应的x值，并指出向量与的位置关系；

(3)若θ为锐角，对于正实数m，关于x的方程有两个不同的正实数解，且x≠m，求m的取值范围.

解题策略　本题是三角与平面向量、函数的最值、方程有实根众多知识的综合，函数与方程思想作为一条红线贯串其中.第(1)小题，依据两向量垂直的充要条件求cosθ的值，进而运用同角三角比基本关系式求sinθ，tanθ之值.第(2)小题转化为二次函数运用配方法求最小值并以此探究向量与的位置关系.第(3)小题将方程转化为x的一元二次方程，通过方程有两个不同实根转化为相应的不等式组，结合三角比的取值范围探求m的取值范围.

解：(1)由题意得即

得32-2×3×1×cosθ-8×12=0,得又θ∈(0，π)，故

因此，

(2)

故当时，的最小值为此时，故向量与垂直.

(3)对方程两边平方整理得9x2-(6cosθ)x+1-9m2=0　　①

设方程①的两个不同正实数解为x1,x2,则由题意得：

若x=m,则方程①就化为-(6cosθ)m+1=0,得而x≠m,故

由得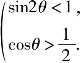得0°<θ<60°且θ≠45°，

当0°<θ<60°且θ≠45°时，m的取值范围为

当60°≤θ<90°或θ=45°时，m的取值范围为