运用函数与方程思想的三大法宝：待定系数法、换元法、转换法

在运用函数与方程思想解题的过程中，在确定函数、方程、不等式的参变数的值时需要运用待定系数法，而构造法又常常与待定系数法紧密相联，换元法往往可以使较为复杂的问题变为基本题型，许多数学问题就是在不断转换的过程中加以解决的.如函数问题可以转换为方程问题求解，方程问题可以转换为函数问题通过图像结合不等式知识求解，善于转换是数学核心素养的体现.

例1　设抛物线y=ax2+bx+c过点A(1,2)和B(-2,-1).

(1)试用a表示b和c；

(2)对于任意非零实数a，抛物线都不过点P(m，m2+1)，试求m的值.

解题策略　对本题题意的理解是关键，什么是抛物线都不过某点呢？换一种说法是：将该点的坐标代入所给的抛物线方程，方程无实数解，所以本题体现了一种等价转换的思想以及待定系数法在研究函数与方程问题中的应用.

解：(1)依题意，解得

(2)y=ax2+(1+a)x+1-2a，将(m,m2+1)代入，得am2+(1+a)m+1-2a=m2+1，整理得(m2+m-2)a=m2-m.

由题意，关于a的方程无非零实数解，

由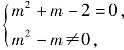得m=-2；由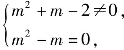得m=0.

故所求的值为m=-2或m=0.

例2　(1)已知数列{an}中，a1=10，且an=15an-1+2·5n，求这个数列的通项公式；

(2)已知数列{an}中，a1=3，a2=5，an=an-2+4n-3(n≥3)，求通项公式an.

解题策略　第(1)问，所给的递推式关系不明朗，应先进行变形，再运用待定系数法构造新的特殊数列，从而使问题获解；第(2)问，一般解法是设待定系数A,即由an+An2=an-2+An2+4n-3配方，得an+An2=an-2+A(n-2)2+(4A+4)n-4A-3,令4A+4=0，解得A=-1，从而构造等差数列.当然，如果直接对递推关系变形很难看出解题者的数学核心素养.

解：(1)先对递推式进行变形，即

设则bn=3bn-1+2.　　①

引入待定系数α，β,使α，β满足bn-β=α(bn-1-β).

展开得bn=αbn-1-αβ+β.　　②

对照①式和②式，可得方程组解得

即数列[bn+1]是以为首项，3为公比的等比数列，

所以bn+1=3·3n-1=3n,bn=3n-1.

于是，

(2)由条件可得an-n2=an-2-(n-2)2+1(n≥3).令bn=an-n2，则数列{bn}可化为两类等差数列，其中{b2n-1}是以b1=a1-1=2为首项，d=1为公差；{b2n}是以b2=a2-22=1为首项，d=1为公差.

因此，b2n-1=2+(n-1)，b2n=1+(n-1).

所以a2n-1=(2n-1)2+n+1，a2n=(2n)2+n.

故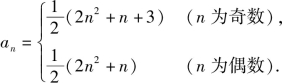

可简化为

例3　设a为实数，函数的最大值为g(a).

(1)设求t的取值范围，并把f(x)表示为t的函数m(t)；

(2)求g(a)；

(3)试求满足的所有实数.

解题策略　本例是一道递进式的综合题，主要考查函数、方程等基础知识，考查分类与整合以及函数与方程的思想方法和综合运用数学知识分析问题、解决问题的能力，难度上循序渐进，第(1)问考查变量代换的技巧，难点在新变量范围的确定，可以有不同的方法求解；第(2)问是含参函数在区间上最大值的求法.分类与整合并结合函数单调性是解答的关键；第(3)问实质是解方程，由于g(a)是分段的，对于方程解的讨论更要分类全面、环环相扣.正如罗素所言：“数学不仅拥有真理，而且还拥有至高的美——一种冷峻而严肃的美，正像雕塑所具有的美一样……”本题的解决过程不仅能显示解题者的数学功力，也展现了“一种冷峻而严肃的美”.

解：(1)解法一　(代数法)令要使t有意义，必须

即-1≤x≤1.

　　①　∴t的取值范围是

由①式得故

解法二　(三角换元法)令

t

由于所以即

又(www.xing528.com)

故

(2)由题意知g(a)即为函数的最大值.

注意到直线t=是抛物线的对称轴，故分以下几种情况讨论.

❶当a>0时，函数的图像是开口向上的一段抛物线，

知m(t)在上单调递增，∴g(a)=m(2)=a+2.

❷当a=0时，

❸当a<0时，函数的图像是开口向下的一段抛物线.

若即则

若即则

若即则g(a)=m(2)=a+2.

综上可得：

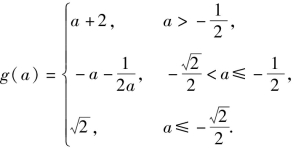
(3)❶当a<-2时，此时

由解得与a<-2矛盾.

❷当时，此时

解得与矛盾.

❸当时，此时所以

❹当时，此时

由即得解得与矛盾.

❺当时，此时

由即得解得与矛盾.

❻当a>0时，此时

由即得解得a=±1，由a>0得a=1.

综上可得，满足的所有实数a为或a=1.

例4　如图3-3所示，设直线l与椭圆相切，切点为P,点M是坐标原点O在直线l上的正投影，求|MP|的最大值和最小值.

解题策略　本例的解答分3步：第一步,求出切线l的方程和直线OM的方程；第二步，求出点M的坐标用点P(x0，y0)的坐标表示，运用两点间距离公式求得关于的函数关系式；第三步，进入求|MP|最值的流程，然而函数解析式太复杂了，可通过换元法变为基本函数求最值问题，当然新元的取值范围一定要紧紧抓住！

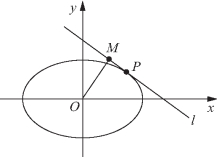
图3-3

解：设P(x0,y0),则(点P在椭圆上)，切线l的方程为x0x+2y0y=2(已知切点求椭圆的切线方程)，

由OM⊥l得直线OM的方程为2y0x-x0y=0.

联立两直线方程，求得点M(x，y)的坐标为

以代入得),

∴=(x-x0)2+(y-y0)2

设=t(0≤t≤1)，则

(由基本不等式求得).

当且仅当即时等号成立.

函数g(t)在区间[0,1]上有最大值最小值0.即|MP|的最大值和最小值分别为