函数与方程、不等式三者之间密切相关、相互转化,利用方程的思想可以通过待定系数法求解函数的解析式.通过把函数等价转化为曲线的方程,借助函数的图像来讨论方程根的个数(或函数零点的个数),由于函数又与不等式有着密切的内在联系,因此研究函数的性质又常常需要用不等式作为工具,如证明(讨论)函数的单调性,讨论函数的最值等.在处理不等式恒成立问题时,经常需要通过构造函数,利用函数的图像或性质进行转化,从而确定相关参数的范围.函数与方程、不等式之间的相互转化不仅表现在二次函数与一元二次方程,一元二次不等式这3个“二次”上,还表现在指数函数,对数函数,指、对数方程和指、对数不等式上,在解题中主要表现在如下4个方面:
(1)对于函数y=f(x),x∈D,我们把使f(x)=0的实数x(x∈D)称为函数y=f(x)的零点,实质上函数y=f(x)的零点就是函数y=f(x)的图像与x轴的公共点的横坐标,也就是方程f(x)=0的根.
(2)若函数y=f(x)在闭区间[a,b]上的图像是连续曲线,并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a,b)内至少有一个实数解.
(3)对于一元二次方程根的研究以及一元二次不等式解集的讨论都可以借助于二次函数的图像找到解题的思路与方法,这就是函数与方程的思想方法.
(4)对于含参数方程f(x,a)=0,有些可以转化为函数a=g(x)的形式;对于含参数不等式f(x,a)>0(或f(x,a)≥0等),有些可以转化为不等式a>g(x)(或a≥g(x)等)的形式,进而通过研究函数g(x)的图像与性质解决相应的问题.反之,有些函数问题则能转化为方程与不等式的问题.
例1 已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的取值范围;
(2)若方程两根均在区间(0,1)内,求m的取值范围.
解题策略 本题由方程根的范围确定方程系数的范围,关键是实施由方程向函数的转化,由函数向不等式的转化,那么如何来实施这二次转化呢?熟知方程的根对于二次函数性质所具有的意义是正确实施转化的核心,在用二次函数的性质结合图形对方程的根进行限制时,应密切注意条件的严谨性,条件不严谨是解答本题的主要困难,务请考虑周全.
解:(1)由题设知抛物线f(x)=x2+2mx+2m+1与x轴的交点分别在区间(-1,0)和(1,2)内,画出二次函数的示意图,如图3-1所示,得

图3-1
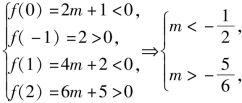 故
故![]()
即m的取值范围为![]()
(2)如图3-2所示,抛物线与x轴交点落在区间(0,1)内,对称轴x=-m在区间(0,1)内通过(千万不能遗漏),可列出不等式组
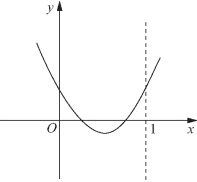
图3-2


于是有![]() 即m的取值范围为
即m的取值范围为![]()
例2 已知a是实数,函数f(x)=2ax2+2x-3-a,如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.
解题策略 零点问题实质是方程根的问题,把函数值为零时的等式看作x的方程.函数y=f(x)在[-1,1]上有零点,即此方程在[-1,1]上有实根(一个解或两个解).再结合图像特征,转化为解不等式,则问题容易解决了.
解:函数y=f(x)在区间[-1,1]上有零点,等价于方程f(x)=2ax2+2x-3-a=0在[-1,1]上有解.
当a=0时,方程f(x)=0是一次方程2x-3=0,解为![]() 不符合题意;
不符合题意;
当a≠0时,方程f(x)=0是二次方程.
方程f(x)=0在[-1,1]上有解,对解的要求是:
❶f(x)=0在[-1,1]上有一个解(另一个解不属于区间[-1,1]),这时应满足:f(-1)f(1)≤0,即(a-5)(a-1)≤0,解得1≤a≤5.
❷f(x)=0在[-1,1]上有两个解(包括有两个等根),这时应满足:
 或a≥5.
或a≥5.
由❶和❷得![]() 或a≥1.
或a≥1.
所以实数a的取值范围是![]()
例3 (1)函数![]() 在[1,2]上恒为正数,则a的取值范围是( );
在[1,2]上恒为正数,则a的取值范围是( );
![]()
(2)(2018年高考浙江卷第17题)已知点P(0,1),椭圆![]() 上两点A,B满足
上两点A,B满足![]() 则当m=________时,点B横坐标的绝对值最大.
则当m=________时,点B横坐标的绝对值最大.
解题策略 第(1)问,依据对数函数的单调性将函数恒为正数转化为一元二次不等式在[1,2]上恒成立问题,采用分离参数的方法转化为耐克函数性质的研究,进而求得参数a的取值范围.第(2)问,表面上是解析几何与平面向量的综合.在一定条件下,曲线方程可看作隐函数,利用向量共线,实现点的坐标之间的转化,结合点在椭圆上,建立方程,结合韦达定理及基本不等式求点B横坐标绝对值的最大值以及相应m的值.也可应用二次函数的最值,求得相应的结论.如果用直线AB的参数方程解,方程理论与基本不等式相结合仍然是解答本题的必用知识,函数与方程的思想体现得相当充分.
解:(1)由题意得,当x∈[1,2]时,![]() 恒成立,故恒有0<x2-ax+3<1.
恒成立,故恒有0<x2-ax+3<1.
∵x∈[1,2],∴由x2-ax+3>0,可得![]()
令![]() 显然函数在
显然函数在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,故其最小值为
上为增函数,故其最小值为![]()
要使不等式![]() 恒成立,则需
恒成立,则需![]()
由x2-ax+3<1,得x2-ax+2<0,又x∈[1,2],故可得![]()
令![]() 该函数在
该函数在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,而h(1)=h(2)=3,故h(x)的最大值为3.要使不等式
上为增函数,而h(1)=h(2)=3,故h(x)的最大值为3.要使不等式![]() 在[1,2]上恒成立,只需a>3.(https://www.xing528.com)
在[1,2]上恒成立,只需a>3.(https://www.xing528.com)
综上所述,a的取值范围是![]() 故选D.
故选D.
(2)解法一 由条件知直线AB的斜率存在,设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1(k≠0),
联立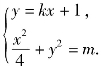 得(4k2+1)x2+8kx+4-4m=0.
得(4k2+1)x2+8kx+4-4m=0.
由韦达定理得![]() ①
①
由![]() 知x1=-2x2,
知x1=-2x2,
代入①式,解得![]() 所以
所以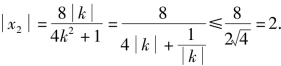
此时![]() 又
又![]() 解得m=5.
解得m=5.
解法二 设A(x1,y1),B(x2,y2),由![]() 得
得![]()
即![]()
因为点A,B在椭圆上,所以 得
得![]()
所以![]() 解得m=5.
解得m=5.
解法三 设直线AB的参数方程为![]() 其中t为参数,α为直线AB的倾斜角,将其代入椭圆方程中化简得(1+3sin2α)t2+8tsinα+4-4m=0,设点A,B对应的参数分别为t1,t2,则t1=-2t2.
其中t为参数,α为直线AB的倾斜角,将其代入椭圆方程中化简得(1+3sin2α)t2+8tsinα+4-4m=0,设点A,B对应的参数分别为t1,t2,则t1=-2t2.
由韦达定理知![]() 解得
解得![]()
所以![]()
 此时cos2α=4sin2α,即
此时cos2α=4sin2α,即![]() 代入
代入![]() 解得m=5.
解得m=5.
例4 已知函数
(1)当0<a<b,且f(a)=f(b)时,求![]() 的值;
的值;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b].若存在,则求出a,b的值;若不存在,请说明理由;
(3)若存在实数a,b(a<b)使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb](m≠0),求m的取值范围.
解题策略 本题初看是分段函数问题,重点是根据函数的性质研究定义域与值域的对应关系,而实质是方程理论贯穿于问题解决的始终,体现了运用函数思想、方程思想解决问题的一种理念.这里,认真读题、缜密审题、确切理解题意、明确问题的实际背景、实施函数向方程的转化探求![]() 的值及m的取值范围.中国大哲学家庄子的名言“判天地之美,析万物之理”,掌握了数学思想就可以“判事物之美,析数量之理”.本题的解答充满了数学思想的激荡,值得细细品味.
的值及m的取值范围.中国大哲学家庄子的名言“判天地之美,析万物之理”,掌握了数学思想就可以“判事物之美,析数量之理”.本题的解答充满了数学思想的激荡,值得细细品味.
解:(1) 在(0,1)上为减函数,在(1,+∞)上为增函数,由0<a<b且f(a)=f(b),可得0<a<1<b且
在(0,1)上为减函数,在(1,+∞)上为增函数,由0<a<b且f(a)=f(b),可得0<a<1<b且![]() 故
故![]()
(2)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,则0<a<b.
❶当a,b∈(0,1)时,![]() 在(0,1)上为减函数.
在(0,1)上为减函数.
故 即
即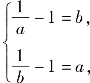 解得a=b,故此时不存在符合条件的实数a,b.
解得a=b,故此时不存在符合条件的实数a,b.
❷当a,b∈[1,+∞)时,![]() 在[1,+∞)上是增函数.
在[1,+∞)上是增函数.
故 即
即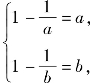 此时,a,b是方程x2-x+1=0的根,此方程无实根,故此时不存在符合条件的实数a,b.
此时,a,b是方程x2-x+1=0的根,此方程无实根,故此时不存在符合条件的实数a,b.
❸当a∈(0,1),b∈[1,+∞)时,
由于1∈[a,b],而f(1)=0∉[a,b],故此时不存在符合条件的实数a,b,
综上可知,不存在符合条件的实数a,b.
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb],且a>0,m>0.
❶当a,b∈(0,1)时,由于f(x)在(0,1)上是减函数,故
此时得![]() 得a=b,与条件矛盾,所以a,b不存在.
得a=b,与条件矛盾,所以a,b不存在.
❷当a∈(0,1),b∈[1,+∞)时,易知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
❸当a,b∈[1,+∞)时,
∵f(x)在[1,+∞)上是增函数,![]() 即
即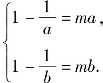
a,b是方程mx2-x+1=0的两个根.
即关于x的方程mx2-x+1=0有两个大于1的实根.
设这两个根为x1,x2.则![]()
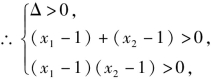 即
即 解得
解得![]()
故m的取值范围是![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




