如果所给出的数学问题从表面上看是非方程问题或给定的方程含有参数或形式较为复杂,就需要凸现其隐含条件,显化方程特征.运用有关方程解的定理(如韦达定理,根的判别式,实根分布的充要条件)使原问题获解,这是方程思想应用的一个重要方面.特别是对于某些非方程问题,通过变形转化成方程问题的过程称之为构造方程法,这是应用方程思想解决非方程问题的一种极富创造的解题策略.
显化或构造方程,运用方程思想解题主要表现在如下4个方面:
(1)转化为解方程或通过不等式讨论根的状况.
(2)转化为带参数的方程或不等式的讨论.常涉及一元二次方程根的判别式、根与系数的关系、区间根、区间上恒成立等知识.
(3)需要转化为方程的讨论、图形的分析、曲线的位置关系等.
(4)构造方程或不等式求解实际应用问题.
例1 函数![]() 的值域是________.
的值域是________.
解题策略 本例是三角函数的值域的求解,由于不是常见的三角函数解析式,需要转化为方程问题,通常是把原函数解析式两边平方得![]() 化正弦为余弦并整理得cos2x+4y2cosx+5y2-1=0,这是关于cosx的一元二次方程,容易想到Δ=(4y2)2-4(5y2-1)≥0,即4y4-5y2+1≥0,解得
化正弦为余弦并整理得cos2x+4y2cosx+5y2-1=0,这是关于cosx的一元二次方程,容易想到Δ=(4y2)2-4(5y2-1)≥0,即4y4-5y2+1≥0,解得![]() 应用方程思想把函数式变为关于cosx的一元二次方程求解思路是正确的,但是还要注意到cosx∈[-1,1],即关于cosx的一元二次方程在[-1,1]上有实根,解数学问题要注意等价转化.
应用方程思想把函数式变为关于cosx的一元二次方程求解思路是正确的,但是还要注意到cosx∈[-1,1],即关于cosx的一元二次方程在[-1,1]上有实根,解数学问题要注意等价转化.
解法一 由![]() 得
得![]() 即1-cos2x=5y2+4y2cosx,整理得cos2x+4y2cosx+5y2-1=0.
即1-cos2x=5y2+4y2cosx,整理得cos2x+4y2cosx+5y2-1=0.
将上述方程看成关于cosx的一元二次方程,∵0≤x≤2π,∴-1≤cosx≤1.设t=cosx,得t2+4y2t+5y2-1=0,
则关于t的一元二次方程在t∈[-1,1]上有实根,令f(t)=t2+4y2t+5y2-1.
∵f(-1)=y2≥0,f(1)=9y2≥0,
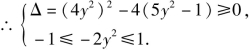 即
即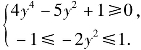 解得
解得![]()
即函数的值域是![]()
解法二 注意到![]() 平方得
平方得![]()
原问题即转化为关于cosx的一元二次方程cos2x+4y2cosx+5y2-1=0在[-1,1]上有实根,求y的取值范围.
只要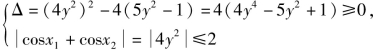
解之得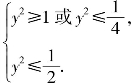 即
即![]() 即函数的值域是
即函数的值域是![]()
例2 已知![]() 求正数
求正数![]() 的最小值.
的最小值.
解题策略 本例求函数的最小值,由于不是常见函数,直接求最值是有困难的,在![]() 的条件下将原函数去分母平方整理为关于x的一元二次方程,再转化为关于x的二次函数在
的条件下将原函数去分母平方整理为关于x的一元二次方程,再转化为关于x的二次函数在![]() 上有解的讨论,体现了函数与方程思想的相互转化,相互补充,提供了构造方程(或函数)解题的又一途径,扩展了解题思维的空间,当然本例也可以变形后直接配方:
上有解的讨论,体现了函数与方程思想的相互转化,相互补充,提供了构造方程(或函数)解题的又一途径,扩展了解题思维的空间,当然本例也可以变形后直接配方:![]() 由
由![]() 得
得![]() 结合二次函数的性质可知,当
结合二次函数的性质可知,当![]() 时,
时,![]()
下面的解法即方程与函数思想的联用:函数→方程→函数.
解:将原函数变形为![]() (https://www.xing528.com)
(https://www.xing528.com)
设f(x)=y2x2-5x+2.该方程有解的主要条件为
①![]() 或②
或②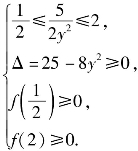 解得
解得![]()
![]() 此时
此时![]() 或x=2.
或x=2.
例3 (1)已知![]() 且
且![]() 求
求![]() 的值;
的值;
(2)设△ABC的三内角A,B,C满足2B=A+C且![]() 求
求![]() 的值.
的值.
解题策略 本例两小题都是在特定条件下的求值问题.第(1)问,题设条件具备x2+x-3=0的形式,如果把![]() 看成该方程的两个根,就可以通过构造二次方程结合韦达定理,使复杂的代数式求值问题简化,从而顺利求解;第(2)问,将
看成该方程的两个根,就可以通过构造二次方程结合韦达定理,使复杂的代数式求值问题简化,从而顺利求解;第(2)问,将![]() 看作一个整体,在此基础上将∠A和∠C用同一个角表示,构造方程使得问题得以解决.当然由条件易得
看作一个整体,在此基础上将∠A和∠C用同一个角表示,构造方程使得问题得以解决.当然由条件易得![]() 则
则![]() 直接代入条件
直接代入条件![]() 得
得![]() 通过和差与积的互化公式得到
通过和差与积的互化公式得到![]() 的一元二次方程,
的一元二次方程,![]() 为系数.利用判别式易得
为系数.利用判别式易得![]() 的值,读者可以一试.
的值,读者可以一试.
解:(1)![]() 且
且![]()
![]() 是方程x2+x-3=0的两个根,即
是方程x2+x-3=0的两个根,即![]()
故![]()
(2)在△ABC中,有A+B+C=π,由2B=A+C可知,![]()
设![]() 则
则![]()
于是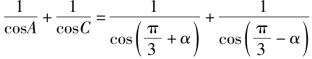
故由题设得![]()
整理得![]() 即
即![]()
![]() 即
即![]()
例4 设x,y为实数,且x2+xy+y2=3,求f(x,y)=x2-xy+y2的最大值和最小值.
解题策略 求二元函数的最大值和最小值,如果采取消元后再求显然难以办到.注意到条件和结论只有xy和x2+y2两种形式,想得到x+y是不困难的.现在要求f(x,y)的最大值和最小值,故可构造一元二次方程且以f(x,y)为参数,则由方程理论f(x,y)的取值范围不难求得.这就告诉我们:一个数学问题中的任何一个数或式都可以视为未知数,而其余的数或式则视为已知数,它们之间的制约关系——等式,即可视为方程.
解:由![]() 可求得
可求得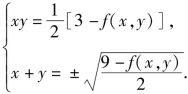
于是x,y是方程![]() 的两个实根,由Δ≥0,得
的两个实根,由Δ≥0,得
f(x,y)≥1;由![]() 得f(x,y)≤9.
得f(x,y)≤9.
故f(x,y)=x2-xy+y2的最大值和最小值分别为9和1.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




