练习构造数列、排列组合和概率模型，用结构思想解题

数学模型是原型的一个相似变换，解题的过程实质上包含着多层次的思维转化过程，如果原型所提供的信息其内在的本质与数列、排列组合、概率有关，那么这个原型可以转化为运用构造法，转化为建立数列、排列组合、概率的数学模型来解.

例1　(1)数列{an}中，a1=1，an+1=2an-3n,求通项an；

(2)设b>0，数列{an}满足求通项an.

解题策略　构造法在解决数列问题中应用非常广泛,第(1)问,形如an+1=pan+q(p≠1,q≠0)的递推式，可由下面两种构造法求通项公式.

方法一　由an+1=pan+q及an=pan-1+q两式相减得an+1-an=p(an-an-1)，有{an+1-an}是首项为a2-a1，公比为p的等比数列，先求an+1-an，再利用“累加法”求an.

方法二　若p=1，则显然是以a1为首项，q为公差的等差数列；若p≠1,p≠0，q≠0.则构造数列{an+λ}满足an+1+λ=p(an+λ)，运用待定系数法，解得则是首项为公比为p的等比数列.

第(1)问，递推式中q=-3n是与n相关的变数，不能用方法一来解，用方法二构造等比数列是可以的，若递推式两边同除以3n+1，也可轻松求解.

第(2)问，形如运用取倒数，构造数列满足从而转换为第(1)问的类型继续求解.

解：(1)解法一　将递推关系式变形为an+1+3n+1=2(an+3n)，

而a1+31=1+3=4.∴{an+3n}是首项为4，公比为2的等比数列.

∴an+3n=4·2n-1=2n+1，∴an=2n+1-3n.

解法二　将递推式an+1=2an-3n两边同除以3n+1，

得令则

令即

而

∴{cn+1}是以为首项，为公比的等比数列.

即

∴an=2n+1-3n.

(2)

当b=1时，有即数列是等差数列.

即an=1.

当b>0且b≠1时，有

又数列是首项为公比为的等比数列，则有

得

故

例2　对负整数a，数4a+3，7a+7，a2+8a+3依次成等差数列.

(1)求a的值；

(2)若数列{an}满足an+1=an+1-2an(n∈N*)，a1=m,求an的通项公式；

(3)在(2)的条件下，若对任意n∈N*，有a2n+1<a2n-1，求m的取值范围.

解题策略　本例考查等差数列的概念、由数列的递推式求通项公式、由数列不等式求参数m的取值范围，三小题环环相扣，前后呼应，若前面小题没有解好，会直接影响后面小题的求解.在第(2)问的求解中可以依据递推关系的特征，用构造法构造特殊数列(等差或等比数列)求通项公式，也可以运用迭代法求解.事实上，迭代法是一种优美的且适用范围更广的解法，其难点是探求迭代后的规律，而构造法的关键是发现递推公式的特点，通过适当的变形构造新数列，由递推关系求通项公式，构造法和迭代法是两种最为基本的解题通法.第(3)问，在有了{an}的通项公式之后，运用含参不等式恒成立的条件实施参变分离，即可求出m的取值范围.

解：(1)依题意有4a+3+a2+8a+3=2(7a+7)，即a2-2a-8=0，

解得a=-2或a=4.∵a<0，∴a=-2.

(2)解法一　(构造法之一：构造等差数列)

原递推式即为

从而数列是以为首项，1为公差的等差数列.

解法二　(构造法之二：构造等比数列)

由an+1=-2an+(-2)n+1，令an+1+λ(n+1)(-2)n+1=-2[an+λn(-2)n]，

比较两式得λ=-1.故原式为an+1-(n+1)(-2)n+1=-2[an-n(-2)n].

数列{an-n(-2)n}是首项为a1+2=m+2，公比为-2的等比数列.

∴an-n(-2)n=(m+2)(-2)n-1，∴an=m·(-2)n-1+(n-1)·(-2)n.(www.xing528.com)

解法三　(迭代法)

由an+1=(-2)n+1-2an得an=-2an-1+(-2)n=-2[-2an-2+(-2)n-1]+(-2)n

=(-2)2an-2+(-2)n+(-2)n=(-2)2[-2an-3+(-2)n-2]+2·(-2)n

=(-2)3an-3+3·(-2)n=…=(-2)n-1a1+(n-1)(-2)n

=m·(-2)n-1+(n-1)·(-2)n.

(3)由a2n+1<a2n-1对n∈N*恒成立得

m·(-2)2n+2n·(-2)2n+1<m·(-2)2n-2+(2n-2)·(-2)2n-1对n∈N*均成立.

∵(-2)2n-2>0，两边同除(-2)2n-2，

得4m+(-8)·2n<m+(-2)·(2n-2)，得对n∈N*恒成立.

当n=1时，最小，为

例3　(1)求证：

(2)求证：

解题策略　在证明组合数等式时，可以先为它设置一个情景，在这个情景下，通过新的知识加以解决.第(1)问，完全通过代数的方法来证明是比较复杂的，根据等式右边我们可以构造这样的情景：“从n+m个不同元素中取出k个元素，共有多少种不同的取法？”第(2)问，同样可以构造一种情景：“从2n个大小相同小球中取出n个小球等价于把2n个小球分为A、B两组，每组n个小球，从A、B两组中共取出n个小球”.

证明　(1)构造情景：“从n+m个不同元素中取出k个元素，共有多少种不同的取法？”直接的方法就是种，也可以分两步来完成，在其中n个元素中，取i个，在另m个元素中取(k-i)个(0≤i≤k，i∈N)，这样原等式显然得证.

(2)一只装有2n个大小相同小球的盒子，从中取出n个小球，共有种取法，也可分两步来完成，将这2n个小球平均分成A、B两组，从中取n个小球，从A中取出0个，则从B中取n个；从A中取1个，则从B中取n-1个；从A中取2个，则从B中取n-2个；……；从A中取n个，则从B中取0个，共有种取法.

本例第(2)问还可以运用概率知识来证明，介绍如下：

设一个袋子中有n个白球和n个黑球，从中任取n个，求P(A)=P(至少有一个白球)，可以这样考虑：

一方面，不取白球的概率为于是有

另一方面，取到k个白球(1≤k≤n且k∈N)的概率为

故有等式两边同乘以并移项即得

例4　(1)袋中有红球和白球共100个，若从这只袋中任取3个球，试问：袋中有n个红球时，能使取出的3个球全为同色的概率为最小？

(2)已知求证：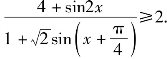

解题策略　把这两道题放在一起颇有意思，第(1)问已是概率题型，若设红、白球的个数分别为x、y，则x+y=100，问题就转化为把任取3个球为同色的概率表示为变量x的函数，构造出函数解析式求概率最小时x的值，其中构造函数的过程是一个难点，需要运用代数恒等变形及消元(消去y)的技巧；第(2)问是三角函数不等式的证明，如何通过构造概率模型来证需要仔细考量，原不等式变形得由于0≤sinx≤1，0≤cosx≤1，对照概率性质0≤P(A)≤1，两者似乎产生了联系，将所证不等式去分母整理得sinx+cosx-sinxcosx≤1，又似乎与概率加法公式P(A+B)=P(A)+P(B)-P(AB)有了联系，让我们试着构造概率模型来证明吧！

解：(1)设红球、白球的个数分别为x，y，则有x+y=100.　　①

从袋中任取3球全为红球的概率等于

同样，全为白球的概率就等于

由于这两个事件是互斥的，从而3个球为同色的概率为

由①可得x3+y3=(x+y)3-3xy(x+y)=106-300xy.

x2+y2=(x+y)2-2xy=104-2xy，从而

由此，当x=50时，P为最小，此时

(2)证明　所证不等式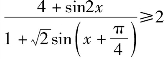变形为

去分母得2+sinxcosx≥1+sinx+cosx.

故只需证明sinx+cosx-sinxcosx≤1.

联想概率加法公式P(A+B)=P(A)+P(B)-P(AB).

设两个独立事件A和B，且P(A)=sinx，P(B)=cosx，由

故0≤sinx≤1，0≤cosx≤1，即0≤P(A)≤1，0≤P(B)≤1,0≤P(AB)≤1.

则P(A+B)=P(A)+P(B)-P(AB)=sinx+cosx-sinxcosx≤1.

∴2+sinxcosx≥1+sinx+cosx.