解析几何的实质是从代数的方向求解几何问题,是将数学问题所呈现的几何特征代数化,如果所给的数学问题从表层看与解析几何毫不相关,则可挖掘题中隐藏的结构特点,通过构造解析几何模型,运用距离公式、斜率公式,点到直线距离公式,直线方程的各种形式以及圆锥曲线方程等巧妙地解决许多数学问题.
当然最为重要的是如何对原型加以分析,产生联想,构造出解析几何模型,并通过求解解析几何模型得到原题的解.
模型法解题必须紧紧抓住以下3点:
(1)构造的数学模型要保证能反映出原命题的本质特征;
(2)构造的数学模型既能进行理性分析,又要能进行计算和逻辑推理;
(3)解答构造的数学模型所获得的结果,一定是原命题的解题目标,并经过检验,对于不符合原命题解题目标的结果应予以舍弃.
例1 (1)试求函数![]() 的最大值;
的最大值;
(2)设θ为锐角,试比较![]() 与tanθ的大小.
与tanθ的大小.
解题策略 第(1)问,除常规解法外还可以构造几何图形,利用斜率求三角函数最值;第(2)问,可以用作差比较法求解,但涉及三角恒等变形,运算量较大,若能注意到两个表达式都与直线的斜率相关,则可应用斜率的几何意义,通过构造图形求解,这样就简捷多了.
解:(1)设点A(cos2α-sinα,sin2α+sinα),点B(3,-1),则y表示A,B两点连线的斜率.
点A的轨迹方程为
![]() 即x+y=1.
即x+y=1.
由于![]() 所以有
所以有![]()
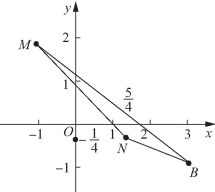
图2-2
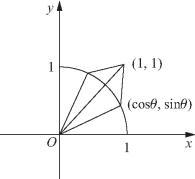
图2-3
故点A的轨迹为线段![]()
![]() 如图2-2所示.
如图2-2所示.
因为![]() 所以
所以![]() 所以
所以![]()
(2)令![]()
其几何意义是单位圆x2+y2=1(x>0,y>0)上
动点与点(1,1)连线的斜率.
又令![]()
其几何意义是单位圆x2+y2=1(x>0,y>0)上动点与原点连线的斜率,如图2-3所示.
从图形中易得
❶ 当![]() 时,0<k2<1<k1,即
时,0<k2<1<k1,即![]()
❷ 当![]() 时,k1=k2=1,即
时,k1=k2=1,即![]()
❸ 当![]() 时,0<k1<1<k2,即
时,0<k1<1<k2,即![]()
例2 (1)求![]() 的最小值;
的最小值;
(2)如果函数![]() 在区间
在区间![]() 上单调递减,那么mn的最大值为( ).
上单调递减,那么mn的最大值为( ).
![]()
解题策略 第(1)问,观察可知,原问题可转化为求两点![]() 间的最短距离的平方.第(2)问,初看是二次型函数的单调性问题,由于解析式含双参数,单从函数角度求解是困难的,必须通过对函数图像的讨论得到关于m,n的不等式组,或通过导函数f′(x)≤0在
间的最短距离的平方.第(2)问,初看是二次型函数的单调性问题,由于解析式含双参数,单从函数角度求解是困难的,必须通过对函数图像的讨论得到关于m,n的不等式组,或通过导函数f′(x)≤0在![]() 上恒成立求得约束条件,求mn的最大值转化为线性规划问题,由动直线与曲线相切或由基本不等式求得.
上恒成立求得约束条件,求mn的最大值转化为线性规划问题,由动直线与曲线相切或由基本不等式求得.
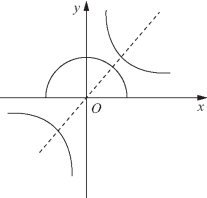
图2-4
解:(1)观察可知,原问题可以转化为求两点![]()
![]() 之间的最短距离的平方.
之间的最短距离的平方.
而这两个动点的参数方程依次是
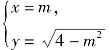 和
和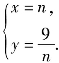 消去m,n得x2+y2=4(y≥0)和xy=9.
消去m,n得x2+y2=4(y≥0)和xy=9.
从而问题进一步转化为求半圆x2+y2=4(y≥0)和双曲线xy=9上的点之间的最短距离的平方,如图2-4所示.
易得![]()
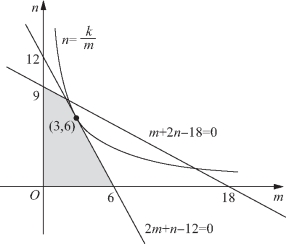
图2-5
(2)解法一 若m=2,则f(x)=(n-8)x+1在![]() 上单调递减,有0≤n≤8;(https://www.xing528.com)
上单调递减,有0≤n≤8;(https://www.xing528.com)
若m>2,则![]() +1为开口向上的二次函数,对称轴为
+1为开口向上的二次函数,对称轴为![]() 有
有![]()
若0≤m<2,则![]() 为开口向下的二次函数,对称轴为
为开口向下的二次函数,对称轴为![]() 有
有![]()
将以上三种情况所得不等式整理即m,n需要满足的约束条件:
![]() 或
或![]() 或
或![]() 作出可行域如图2-5所示的阴影部分,令k=mn,则
作出可行域如图2-5所示的阴影部分,令k=mn,则![]() 表示一簇反比例函数的图像,由计算可知,当反比例函数
表示一簇反比例函数的图像,由计算可知,当反比例函数![]() 与直线2m+n-12=0相切时,k最大,此时切点为(3,6),k的最大值为18,故选B.
与直线2m+n-12=0相切时,k最大,此时切点为(3,6),k的最大值为18,故选B.
解法二 由题意得f′(x)=(m-2)x+(n-8)≤0对任意的![]() 恒成立,∴只需
恒成立,∴只需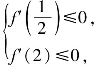 即
即![]() 又m≥0,n≥0,则0≤n≤12-2m,
又m≥0,n≥0,则0≤n≤12-2m,
mn≤m(12-2m).
设![]() 当且仅当m=6-m,m=3,n=6时,等号成立.经检验
当且仅当m=6-m,m=3,n=6时,等号成立.经检验![]() 满足上述条件.
满足上述条件.
故mn的最大值为18,故选B.
例3 (1)求二元函数![]() 的最小值;
的最小值;
(2)已知![]() 求|3x-4y-100|的最值.
求|3x-4y-100|的最值.
解题策略 第(1)问,观察二元函数解析式的结构特点,很像两点之间距离公式的平方,由此可试着构造图形,利用解析几何知识求解,若把二元函数看作关于x的二次函数,y为参数,则可利用二次函数极值法求解.第(2)问,所给条件等式为动点P(x,y)到两定点A(0,0),B(8,6)的距离之和为定长20.由于|AB|=10<20,则点P的轨迹为椭圆.而3x-4y-100=0是一条确定的直线,问题就转化为椭圆上动点到定直线距离的最值.本题的几何意义是求出与长轴所在直线3x-4y=0平行且与椭圆相切的两条直线![]() 它们与直线3x-4y-100=0的距离即为所求的最值.
它们与直线3x-4y-100=0的距离即为所求的最值.
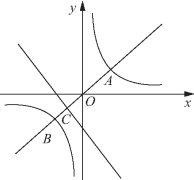
图2-6
解:(1)解法一 (构造法)由二元函数结构特点,可将函数关系看成是点P(x,-x-1)和点![]() 的距离,而点P(x,-x-1)的轨迹是直线x+y+1=0,点
的距离,而点P(x,-x-1)的轨迹是直线x+y+1=0,点![]() 的轨迹是双曲线xy=1,所以问题就转化为直线x+y+1=0上的点和双曲线xy=1上的点的距离平方的最小值.
的轨迹是双曲线xy=1,所以问题就转化为直线x+y+1=0上的点和双曲线xy=1上的点的距离平方的最小值.
如图2-6所示,AB连线过原点且与直线x+y+1=0垂直时,其交点C到点B最近,此时,A、B、C3点的坐标是![]() 即F(x,y)的最小值是
即F(x,y)的最小值是![]()
解法二 (二次函数极值法)首先把原函数看成关于x的二次函数
![]()
顶点在![]()
所以![]() 即F(x,y)的最小值是
即F(x,y)的最小值是![]()
(2)设P(x,y),A(0,0),B(8,6),|AB|=10,则2a=20,2c=10.即![]() 为中心在(4,3),焦点在直线
为中心在(4,3),焦点在直线![]() 上的椭圆.其方程为
上的椭圆.其方程为![]()
设与直线![]() 平行的直线方程为
平行的直线方程为![]() 要使椭圆与直线
要使椭圆与直线![]() 有公共点的m的取值范围是原点到直线
有公共点的m的取值范围是原点到直线![]() 的距离不超过
的距离不超过![]() (即b的值)即
(即b的值)即![]()
解得![]() 椭圆上任意点P(x,y)均满足
椭圆上任意点P(x,y)均满足![]()
由![]() 得
得
![]()
故|3x-4y-100|的最大值为![]() 最小值为
最小值为![]()
例4 在平面直角坐标系xOy中,设定点A(a,a),P是函数![]() 图像上一动点,若点P,A之间的最短距离为
图像上一动点,若点P,A之间的最短距离为![]() 则满足条件的实数a的所有值为________.
则满足条件的实数a的所有值为________.
解题策略 从题目提供的信息:P是函数![]() 图像上一动点,A(a,a)为定点,
图像上一动点,A(a,a)为定点,![]() 构思解题方法可以朝函数方向靠拢,也可以朝解析几何方向靠拢,于是就有了两种不同的构造方法.
构思解题方法可以朝函数方向靠拢,也可以朝解析几何方向靠拢,于是就有了两种不同的构造方法.
思考一 (函数方向)PA的长度可用![]() 和(a,a)两点之间的距离表示,势必会出现
和(a,a)两点之间的距离表示,势必会出现![]() 的形式,通过换元
的形式,通过换元![]() 求解新元t的取值范围,将题目转化为在新元的范围内对二次函数分类讨论求最值,从而确定a的取值.
求解新元t的取值范围,将题目转化为在新元的范围内对二次函数分类讨论求最值,从而确定a的取值.
思考二 (解析几何方向)![]() 为动点,A为定点,不难发现P的轨迹是以(a,a)为圆心,半径为
为动点,A为定点,不难发现P的轨迹是以(a,a)为圆心,半径为![]() 的圆,则原问题就转化为圆(x-a)2+(y-a)2=8与曲线
的圆,则原问题就转化为圆(x-a)2+(y-a)2=8与曲线![]() 相切的问题,联立消y之后可利用方程根的判别式解决.
相切的问题,联立消y之后可利用方程根的判别式解决.
解法一 设![]() 则
则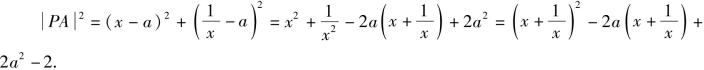
令![]() 得t≥2,
得t≥2,![]() =t2-2at+2a2-2=(t-a)2+a2-2.
=t2-2at+2a2-2=(t-a)2+a2-2.
当a<2时,![]()
当a≥2时,![]()
解得a=-1或![]()
解法二 由题意可知,若a<0,则a=-1满足题意;
若a>0,则圆(x-a)2+(y-a)2=8与![]() 相切,
相切,
联立方程组,消去y得![]()
即![]() ①
①
令Δ=0,得(2a)2-4(2a2-10)=0,解得![]()
此时方程①的解为![]() 满足题意.
满足题意.
综上,实数a的所有值为![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




