巧用结构思想解题：构造函数、方程、不等式模型解析

构造某种数学模型简称为模型法，而模型是一种结构，这种结构是通过对原型的形象化或模拟与抽象而来的.它的思维程式是：问题→转化为已知的数学模型→应用已知数学模型的某些特征→问题的解决，如图2-1所示.

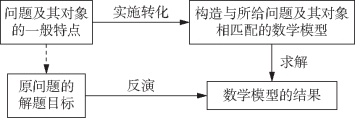
图2-1　模型法

本专题主要以例题来阐述如何根据已知条件和结论，构造函数、方程、不等式数学模型，实施转化解题.

例1　(1)已知a>b>0，求证：

(2)求证:

解题策略　若所证不等式两边符合某一函数在不同自变量时的取值特征，可构造函数，利用函数的性质来证明.第(1)问，所证不等式两边都是的结构，故可设函数为通过函数的单调性证明；第(2)问，所证不等式两边都是的结构，故可设函数为也可通过函数单调性证明.

解：(1)证明　设

因为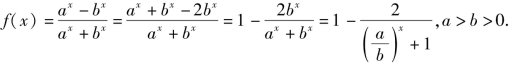

因为所以函数在R上是增函数.

所以f(x)在R上是增函数，所以即

(2)证明　观察所证不等式左、右两边，各项的式子外形结构皆相似于的形式，构造函数

即由于在[0，+∞)上单调递减，因而f(x)在[0，+∞)上单调递增.

令x1=|a+b|，x2=|a|+|b|，则有x1≤x2，f(x1)≤f(x2),

即

例2　(1)若求证：

(2)已知数列{an}，an=2n-1，是否存在正数k，使对一切n∈N*，不等式均成立.若存在，求出k的最大值.若不存在，说明理由.

解题策略　第(1)问，条件a2<a-b即为b<a-a2,0<a<.要证,则可构造二次函数f(a)=a-a2,则可利用二次函数的单调性结合不等式的基本性质完成证明.而第(2)问，所证不等式两边都与n相关，可采用由特殊到一般的方法.先猜测k的最大值，然后用数学归纳法证明，但证明过程相对烦琐，若构造函数，运用函数的有关性质解题往往可以得到简捷的解法.

解：(1)证明　由已知a2<a-b,则

构造一次函数

则f(a)在内为增函数，

又

即

(2)这样的k是存在的.

设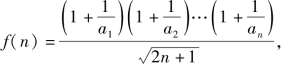

则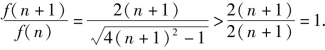

所以f(n)单调递增，f(1)为f(n)的最小值.(www.xing528.com)

因为f(n)≥k恒成立，所以所以k的最大值为

例3　(1)已知实数x，y，z满足x=6-y，z2=xy-9，求证：x=y；

(2)若p，q≥0，且p3+q3=m，求证：

解题策略　第(1)问，由条件易得x+y=6，xy=z2+9，构造以x、y为两实根的方程，运用方程理论求解；第(2)问，设p+q=k，由条件p3+q3=m变形并把p+q=k代入，可使pq用k及m表示，构造以p、q为两非负实根的方程.寻求等价条件求得p+q的取值范围.

证明　由条件得x+y=6，xy=z2+9.由方程根与系数的关系构造以x，y为两根的二次方程：t2-6t+(z2+9)=0　　①

∵Δ=36-4(z2+9)=-4z2≤0.

又方程①有两实根x，y，∴Δ≥0，故Δ=0，从而方程两根相等，即x=y.

(2)证明　∵p3+q3=(p+q)3-3pq(p+q)=m，设p+q=k　　①

则　　②

由①式及②式构造一元二次方程　　③

因方程③有两非负实根，故

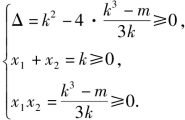解得即

例4　已知α，β为两相异锐角，且满足方程acos2x+bsin2x=c.

求证：

解题策略　本例可以通过适当构造新方程来证，而构造的方程不一样，证法繁简也不一样.证法一通过构造一元二次方程结合韦达定理求证；证法二通过构造直线方程，由点到直线的距离求证.

证法一　由条件移项得acos2x=c-bsin2x.

两边平方变形可得方程(a2+b2)sin22x-2bcsin2x+c2-a2=0.

根据条件sin2α、sin2β是方程(a2+b2)y2-2bcy+c2-a2=0的根.

由韦达定理得，同理可得

证法二　由题设知，点A(cos2α，sin2α)和点B(cos2β，sin2β)所在的直线方程是

ax+by-c=0　　①

经过A、B两点的直线方程还可以表示为

即xcos(α+β)+ysin(α+β)-cos(α-β)=0　　②

由于①②表示同一条直线，因而原点到两直线距离相等.

所以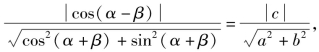即