用综合与分析相结合求解数学问题的讲座

运用分析法与综合法的解题过程如图1-2所示，其中内环是分析过程(执果索因)，外环是综合过程(由因索果).

图1-2　运用分析法与综合法的解题过程

分析与综合思想方法的主要特点如下：

(1)方法上的相互依存、相互补充；

(2)过程中的互相交替、相互转化；

(3)结论在相反的推导过程中得到验证.

分析与综合是两个方向相反的思维过程的统一，其中每一个过程之所以能够进行，就是因为：分析在自身中包含着综合，综合在自身中包含着分析，对于较为复杂的数学问题的解(证)常常是分析，综合两法兼用或者是先用分析法探求解题的起点，找到起点后再用综合法叙述解题(或证明)过程.

例1　已知a>0，b>0，且a+b=1，求证：

解题策略　本例有多种证法，可采用综合法(由因导果)，也可采用分析法(执果索因).当然由条件的特点，采用三角换元结合函数的单调性也是一种好方法.若在证明过程中构造“耐克”函数，利用“耐克”函数的单调性，则使证明“别开生面”且相对简捷，这是本例的妙思巧证.

证法一　(综合法)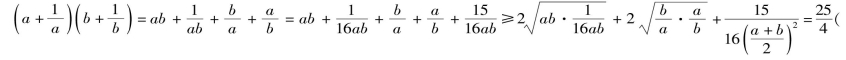在用综合法证题过程中采用拆项不易想到)

证法二　(分析法)欲证原不等式成立，即证

也即证4(ab)2+4(a2+b2)-25ab+4≥0　　①

∵a+b=1，故a2+b2=(a+b)2-2ab=1-2ab　　②

将②式代入①式，得4(ab)2+4(1-2ab)-25ab+4≥0，即证4(ab)2-33ab+8≥0，

也即证或ab≥8，而ab≥8不可能成立，故即证

由a>0，b>0且得因此原不等式成立.

证法三　(三角换元结合函数单调性)令a=sin2θ，b=cos2θ(0<θ<π).

则

令t=sin22θ，∵0<θ<π，∴0<t≤1，设

当0<t1<t2≤1时，

∴y1>y2.即在0<t≤1上为减函数，∴y≥33.

当且仅当a=b时等号成立.

证法四　将展开得这3个式子完全类似，∴可类比构造函数

当x∈(0,1)时，f′(x)<0,∴f(x)在(0,1)上是减函数，

又即

∴

即原不等式成立.

例2　已知函数f(x)=log2(x+2)，a，b，c是两两不相等的正数，且a，b，c成等比数列，试判断f(a)+f(c)与2f(b)的大小关系，并证明该结论.

解题策略　综合法和分析法各有其优缺点，分析法利于思考，综合法宜于表达，因此，在实际解题时，常常把分析法和综合法结合起来运用,先以分析法为主寻求解题思路，再用综合法表述解答或证明过程.两种方法只是解题思维的切入口不同而已，有时要把分析法和综合法结合起来交替使用，才能成功.

本例的求解过程，便是先举特例猜测结论，再用分析法给出思路，最后用综合法给出证明.

取a=1，b=2，c=4，则f(a)+f(c)=f(1)+f(4)=log23+log26=log218，2f(b)=2f(2)=2log24=log216，于是由log218>log216猜测f(a)+f(c)>2f(b).

要证明f(a)+f(c)>2f(b)，则只需证log2(a+2)+log2(c+2)>2log2(b+2)，

即证log2[(a+2)(c+2)]>log2(b+2)2，亦即证(a+2)(c+2)>(b+2)2，

展开整理得ac+2(a+c)>b2+4b，因为b2=ac，所以只要证显然是成立的.

上面从取a=1，b=2，c=4开始到推得的过程就是分析法，下面给出的是运用综合法证明.

解：f(a)+f(c)>2f(b).

证明　因为a，b，c是两两不相等的正数，所以(www.xing528.com)

因为b2=ac，所以ac+2(a+c)>b2+4b.

即ac+2(a+c)+4>b2+4b+4，从而(a+2)(c+2)>(b+2)2，

因为f(x)=log2(x+2)是增函数，所以log2[(a+2)(c+2)]>log2(b+2)2，

即log2(a+2)+log2(c+2)>2log2(b+2).

故f(a)+f(c)>2f(b).

例3　设函数曲线y=f(x)在点(1，f(1))处的切线为y=e(x-1)+2.

(1)求a，b；

(2)证明：f(x)>1.

解题策略　第(1)问运用综合法解很简单，第(2)问相对而言条件复杂而所证结论简单，运用综合法困难较多，运用分析法较易找到证题思路.由于函数f(x)=aexlnx+ex-1的结构较为复杂，在进行分析法证明f(x)>1的过程中技巧性强，这是一道用分析法寻找解题思路的典型案例.

解：(1)函数f(x)的定义域为

由题意可得f(1)=2，f′(1)=e，故a=1，b=2.

(2)证法一　由(1)知

要证f(x)>1，即证　　①

两边同除以ex-1，即证　　②(这一步很难想到)

观察②式的结构，不等式中有3个性质完全不同的项，尝试将它们转化为同型.

当x>0时，ex>x+1，变量代换.用x-1代替x，可得ex-1>x，

即　　③

故只需证即证　　④

这只需证

令则令g′(x)=0，得

当时，g′(x)<0，g(x)在区间上递减；当时，g′(x)>0，g(x)在区间上递增，故

于是，④式成立，即原不等式成立.

证法二　由于x>0，要证f(x)>1，即证

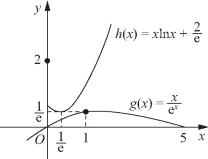
图1-3

即证xexlnx+2xex-1>x，即证

令考察两个函数的单调性，h′(x)=lnx+1，

所以h(x)在上单调递减，在上单调递增(如图1-3所示).

所以

所以g(x)在(0，1)上单调递增，在(1，+∞)上单调递减，所以

由于h(x)与g(x)取得最值时的x值不同，因此h(x)>g(x)恒成立，故原命题成立.

上面的两种证法运用的都是分析法，其中证法二突破了只构造一个辅助函数来解决问题的常规思维，构造了两个函数，一个有最小值，一个有最大值，解法巧妙，这里运用了变式处理的解题策略，若心中存在“模型”意识，这种构造法顺理成章.下面试着用综合法证明，困难在于变形的思路很难想到，一旦想到了反而简单.

证法三　易证明ex≥x+1(当且仅当x=0时取等号).

因为ex≥x+1，所以ex-1≥x，即ex≥ex，故(当且仅当x=1时，取等号)　　①

由ex-1≥x得即

两边取以e为底的对数，得

所以　　②

由于①②式等号不能同时成立，两式相加，得

两边同乘以ex，得f(x)>1.