以综合法为主导的解、证数学问题的优化方式

综合法又称顺推法，是由已知条件(或真命题)推导到未知(或结论)的证明方法，即从已知条件或真命题出发，依次推导出一系列真实命题，最后达到所要证明的命题的结论.

综合法的优点是叙述过程简短明了，缺点是不易找到解决问题的起点(即从哪里开始).

例1　已知a，b，c均为正数，证明：并确定a，b，c为何值时，等号成立.

解题策略　用综合法证明不等式是“由因导果”，这个“因”可以是题中的条件，也可以是已知的公式，本例的证明就是从基本不等式出发推出需证的不等式.那么从三元的基本不等式出发还是从二元的基本不等式出发呢？都是可以的，于是就有了下面两种综合法的证明.

证法一　∵a，b，c均为正数，由三元基本不等式得　　①

　　②

故

又　　③

∴原不等式成立，

当且仅当a=b=c时，①式和②式等号成立.

当且仅当时，③式等号成立.

即当且仅当时，原式等号成立.

证法二　∵a，b，c均为正数，由基本不等式得a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ac，

∴a2+b2+c2≥ab+bc+ac　　①

同理　　②

故

　　③

∴原不等式成立.

当且仅当a=b=c时，①式和②式等号成立，当且仅当a=b=c，(ab)2=(bc)2=(ac)2=3时，③式等号成立.

即当且仅当时，原式等号成立.

例2　已知二次函数f(x)=ax2+bx+c.

(1)若a>b>c且f(1)=0，证明：f(x)的图像与x轴有两个相异交点；

(2)若x1，x2∈R且x1<x2，f(x1)≠f(x2)，证明：方程必有实根在区间(x1，x2)内；

(3)在(1)的条件下，设两交点为A，B，求线段AB长的取值范围.

解题策略　本例以二次函数为载体证明函数图像与x轴的交点问题以及相关方程根的位置，由于二次函数的图像特征很明确，从条件出发运用综合法证明是十分自然的.

证明　由f(1)=0，可得a+b+c=0，由a>b>c，可得a>0，c<0.

∵Δ=b2-4ac=(a+c)2-4ac=(a-c)2>0,

∴f(x)的图像与x轴有两个相异交点.

(2)证明　令

则

又g(x)的图像是连续的，∴方程即g(x)=0必有一实根在区间(x1，x2)内.

(3)设f(x)=0的两根为x1，x2，∵a>b>c，b=-a-c，∴a>-a-c>c.

又

又

长的取值范围为

例3　(清华大学等五校联考试题)已知f(x)是定义在R上的奇函数，且当x<0时，f(x)单调递增，f(-1)=0，设φ(x)=sin2x+mcosx-2m，集合对任意的对任意的求M∩N.

解题策略　本题的求解运用综合法，即从f(x)的性质入手探求集合M，N，再求M∩N，如果在审题时作出函数f(x)的示意图，则对于我们探明M∩N所含元素的特征有很大帮助.为了切实求出M∩N，可运用换元法使之转化为含参数不等式在区间上恒成立问题.为求参数m的取值范围采取参变分离法结合导数求解，也可以变形后由基本不等式求.

解：f(x)是定义在R上的奇函数，且当x<0时，f(x)单调递增，f(-1)=0，所以当x>0时，f(x)也单调递增，且f(1)=0，于是f(x)<0等价于x<-1或0<x<1.(www.xing528.com)

N

而已知

由φ(x)<-1得cos2x-mcosx+2m-2>0.

令t=cosx,则0≤t≤1，于是问题等价转化为：

当不等式t2-mt+2m-2>0在t∈[0，1]上恒成立时，求实数m的取值范围.

由t2-mt+2m-2>0(0≤t≤1)得

设

解法一　对函数h(t)求导，则令h′(t)=0，解得或(舍去).

当时，h′(t)>0，h(t)为增函数；

当时，h′(t)<0，h(t)为减函数；

当时，h(t)取得[0，1]上的最大值故

解法二当且仅当时，取等号).

图1-1

故

例4　设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1，0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(1)证明：|EA|+|EB|为定值，并写出点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围.

解题策略　第(1)问，由平面几何知识易得|EA|+|EB|等于圆A的半径，隐含地告知点E的轨迹为椭圆(不包括x轴上的两点)；第(2)问，当l与x轴不垂直时，设出直线l的方程，与(1)中求出的椭圆方程联立，利用方程根与系数的关系，求出|MN|关于斜率k的表达式，再求出|PQ|关于k的表达式，进而可得四边形MPNQ的面积S关于k的表达式，最后将问题转化为求函数的值域，整个解题过程从条件出发步步推进，由因探果，第一步：求弦长.第二步：求面积表达式.第三步：求范围.还要考虑当l与x轴垂直的情况，此时易得S的值，从而问题圆满解决.本题两问用的都是综合法的解题方法，如果解题中避开对直线斜率的讨论，可设l的方程为x=ky+1的形式，但此时的k不再表示斜率，解题者应当有清晰的认识.

证明　如图1-1所示，∵|AC|=|AD|,EB∥AC，故∠EBD=∠ACD=∠ADC，

∴|EB|=|ED|,

故|EA|+|EB|=|EA|+|ED|=|AD|，又圆A的标准方程为(x+1)2+y2=16，

从而|AD|=4，∴|EA|+|EB|=4.

由题设得A(-1，0)，B(1，0)，|AB|=2，由椭圆定义可得点E的轨迹方程为

(2)第一步：求弦长.当l与x轴不垂直时，设l的方程为y=k(x-1)(k≠0),

M(x1，y1)，N(x2，y2).

由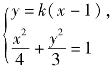得(4k2+3)x2-8k2x+4k2-12=0，则

过点B(1，0)且与l垂直的直线m方程为

∵点A到直线m的距离为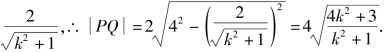

第二步：求面积表达式.

∵待求四边形MPNQ的对角线满足MN⊥PQ.

第三步：求范围.

当l与x轴不垂直时，由上述四边形MPNQ面积的表达式容易求得其取值范围为

当l与x轴垂直时，其方程为x=1，|MN|=3，|PQ|=8，此时四边形MPNQ的面积为12.

综上所述，四边形MPNQ面积的取值范围为