以分析法为主导解、证数学问题

分析法，又称逆推法，是由未知(或结论)追溯到已知条件或真命题的证明方法，即从要证明的结论出发，依次追溯出一系列使结论成立的等价命题，当追溯出的等价命题是已知条件或真命题时，说明结论的真实性，从而证明了原命题的正确性.

分析法的优点是思考问题的解题思路比较自然，问题容易得到解决，缺点是叙述过程比较烦琐.

例1　设a,b,c∈R+，求证：

解题策略　本例是武汉大学自招试题，需证的不等式由多个分式组成且字母又多，若运用综合法，即从左边证到右边，则根本无法入手，因此需要结合分析法，化繁为简.为减少运算量，可先移项通分后再展开对消，容易得到一个显然成立的结果，故本例采用分析法证明是上策.

证明　欲证明原不等式成立，只需证

即证

即证(b+c+2bc+abc+bc2)(1+a+ab)≤(1+ab)(1+b+c+2bc+abc+bc2+ca+abc2)，

即证2abc≤1+a2b2c2,即证(abc-1)2≥0,而此式显然成立，故原不等式得证.

例2　在△ABC中，

(1)求sinA的值；

(2)设△ABC的面积求BC的长.

解题策略　分析法并非局限于证明题，在计算题中同样适用.第(1)问，欲求sinA的值.由sinA=sin(B+C)=sinBcosC+cosBsinC且cosB，cosC的值已知，再求出sinB，sinC的值即可.第(2)问，欲求BC的长.由正弦定理得可推得 而sinA，sinB，sinC的值在第(1)问中已求得，只需求AC·AB或AC·AB·sinA的值，而由则AC·AB·sinA的值可整体求得，这是一道运用分析法解题的典型题目.

解：(1)(先分析)欲求sinA的值，∵sinA=sin(B+C)=sinBcosC+cosBsinC,故需求sinB，sinC的值.

(再综合)

(2)(先分析)欲求BC的长，由正弦定理可得

由(1)得

故只需求AC·AB·sinA的值.

(再综合)由已知得AB·AC·sinA=33.

则

例3　若a，b，c是不全相等的正数，求证：

解题策略　在证明不等式的过程中，分析法和综合法是不可分离的，前者是逆推或倒溯，后者是顺推，如果使用综合法证明不等式难以入手时，常用分析法探索证题途径，然后用综合法的形式写出它的证明过程.有些问题证明难度较大，常常是分析与综合交替使用，比如上例的解法就是如此，也有题目分析法、综合法两法并进，实现两头往中间靠以达到证题目的，称之为“中途岛法”.本例的证明先要利用对数运算变形，把真数从对数中剥离出来，将原不等式转化为再用基本不等式证明.下面介绍分析法与综合法两种证法.事实上，若没有对所证不等式的“剥离”变形，综合法很难想到.

证法一　(分析法)要证

即证成立.

只需证

又

　　①

又∵a，b，c是不全相等的正数，∴①式等号不成立.

∴原不等式成立.(www.xing528.com)

证法二　(综合法)

又∵a，b，c为不全相等的正数，

即

例4　将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表：

a1

a2　a3

a4　a5　a6

a7　a8　a9　a10

……

记表中的第一列数a1，a2，a4，a7，…构成数列为{bn}，b1=a1=1,Sn为数列{bn}的前n项和，且满足

(1)证明数列成等差数列，并求数列{bn}的通项公式；

(2)上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数，当时，求上表中第k(k≥3)行所有项的和.

解题策略　本例以三角形数表和恒等式综合呈现，首先要分析恒等式的结构特征，用换元法bn=Sn-Sn-1转化题设中的恒等式为含Sn，Sn-1的形式，再整理可得(常数)，这是第(1)问的证明思路.而第(2)问的解题关键是先分析三角形数表中an下标序码n的规律，即探索a81在三角形数表中的位置，可用尝试法探知三角形数表中第k行最后一个数的下标序码为当k=12，13时，分别得78，91.由78<81<91知a81是第13行第3个数.也可运用解不等式的方法进行分析探索，即解得又k∈N*,可得k=13，可见分析法在本题的解答中起到重要作用.

解：(1)证明　(先分析，再转化)由已知，当n≥2时，又Sn=b1+b2+…+bn，bn=Sn-Sn-1.

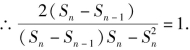即即

得又S1=b1=a1=1.

∴数列是首项公差为的等差数列.

通项为即且

当n≥2时，而b1=1.

因此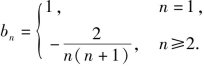

(2)(先分析，后尝试探究，列方程求公比，再综合)首先确定a81是三角形数表中的第几行第几个数.

三角形数表中第k行最后一个数的下标序码为

当k=12,13时，分别计算得78,91两个数.

由78<81<91知a81是第13行第3个数，即a79，a80，a81，…，而三角形数表中第13行第1个数为设从第3行起，每行的公比都为q，

由得解得q=2(取q>0).

三角形数表中第k行第1个数为bk，那么该行所有项(实为k项)的和为