弱式有效市场的检验与优化

检验弱式有效市场的相关文献，多数从时序收益的可预测性和截面收益的可预测性来检验市场是否弱式有效。时序收益的可预测性，又可细分为历史收益预测和外生变量预测；截面收益的可预测性，又可细分为SLB模型、多因子模型、基于消费的资产定价模型。

（一）时序收益的可预测性

1.历史收益预测

有效市场假说的早期实证文献均假设：股票的短期收益是恒定的，并不随时间变化而变化。市场有效表明，股票的历史收益或其他外生变量不可用于预测股票的短期收益，对股票短期收益的最佳预测便是其历史均值。譬如，Fama（1965^[8]）计算了1957年年底至1962年9月道琼斯30种工业股票收益的自相关系数，发现30种工业股票大多并不显著相关，由此证明了弱式有效市场假说成立。

而Lo＆MacKinlay（1988^[9]）、Conrad＆Kaul（1988^[10]）将纽约证券交易所的股票按公司规模分组后发现，股票收益呈显著的正相关关系，且小公司股票的正相关关系更强。最近的相关文献均指出，股票的短期收益（包括日收益、周收益、月收益）均可用历史收益来进行预测，因而股票的短期收益并非恒定不变。

有鉴于此，对有效市场假说的实证研究转入了对股票长期收益的研究。Shiller（1984^[11]）、Summers（1986^[12]）指出，股票的价值不随时间变化而变化，股票价格的无条件均值即为股票的价值，股票价格围绕其价值上下波动且长期均值回复。然而，Stambaugh（1986^[13]）指出，股票价格的长期均值回复意味着股票长期收益具有显著的负自相关性。DeBondt＆Thaler（1985^[14]，1987^[15]）亦指出，股票具有显著的“输家赢家效应”，即前期的绝对输家将会在后期成为赢家，赢得高于市场的回报。对此，Fama＆French（1988^[16]）强调，在研究时序收益的可预测性时，最大问题是无法从股票价格中区分非理性的泡沫和理性的预期收益。

2.外生变量预测

某些外生变量有助于预测股票的短期收益，诸如预期通货膨胀率（Bodie，1976^[17]；Nelson，1976^[18]；Jaffe＆Mandelker，1976^[19]；Fama，1981^[20]）、短期利率（Fama＆Schwert，1977^[21]）、股息收益（DIP）（Rozeff，1984^[22]；Shiller，1984^[23]）、股息价格比（D/P）（Fama＆French，1988^[24]）、收益价格比（E/P）（Campbell＆Shiller，1988^[25]）、消费收入比（CAY）（Lettau＆Ludvigson，2001^[26]）等。然而，外生变量对短期收益的可预测性，并不能表明市场无效。Fama（1991^[27]）指出，外生变量对短期收益的可预测性，实质上是外生变量和短期收益具有高度的相关性，而此相关性并不能表明外生变量对短期收益的可预测性，而极可能是由市场泡沫所致。

但另有文献从市场异象的视角来否定弱式有效市场假说，诸如周末效应（Cross，1973^[28]；French，1980^[29]；Gibbons＆Hess，1981^[30]）、节日效应（Ariel，1990^[31]）、月末效应（Ariel，1987^[32]）、日内效应（Harris，1986^[33]）、小公司效应（Banz，1981^[34]）。

（二）截面收益的可预测性

1.SLB模型

Black、Jensen、Scholes（1972^[35]）、Blume、Friend（1973^[36]）、Fama、MacBeth（1973^[37]）使用SLB模型对截面收益的可预测性做了第一次有益的尝试。SLB模型的早期研究表明：（1）股票预期收益与市场组合收益正相关，相关系数为β；（2）β系数是解释截面预期收益所需风险的唯一度量。(https://www.xing528.com)

批评SLB模型的实证研究始于20世纪70年代后期，此类研究旨在识别足以解释截面预期收益的变量，如收益价格比（Basu，1977^[38]，1983^[39]）、公司规模（Banz，1981^[40]）、账面市值比（Chan、Hamao、Lakonishok，1991^[41]；Fama＆French，1992^[42]）、杠杆率（Chan、Chen，1988^[43]）

然而，由于面临联合检验问题，收益价格比、公司规模、账面市值比、杠杆率与预期收益之间的关系，并非是有效的证据可证明市场不有效，因为人们无法认定此类研究结果是市场真的不有效抑或是资产定价的错误。

2.多因子模型

在SLB模型中，证券和投资组合的截面预期收益系由市场β系数决定。多因子模型的早期文献多使用宏观变量因子（Chen、Roll、Ross，1986^[44]）和统计因子（Chamberland＆Rothchild，1986^[45]；Connor＆Korajczyk，1987^[46]）来研究截面收益的可预测性。而Fama＆French（1992^[47]，1993^[48]，1996^[49]）指出，账面市值比和公司规模比β系数能更好地解释股票的截面预期收益，于是将账面市值比和公司规模引入SLB模型，构建了Fama-French三因子模型。此后，诸多因子被引入用于解释截面收益的可预测性，如动量因子（Carhart，1997^[50]）、流动性风险因子（Pastor＆Stambaugh，2003^[51]）、投资因子（Hou、Xue＆Zhang，2015^[52]；Fama＆French，2015^[53]）等。而Daniel＆Titman（1997^[54]）质疑了多因子模型，他们认为多因子模型无法识别是因子所代表的股票风险驱动了股票收益抑或是因子所代表的股票特质恰好与股票收益相关。

3.基于消费的资产定价模型

Rubinstein（1976^[55]）、Lucas（1978^[56]）、Breeden（1979^[57]）等提出了基于消费的资产定价模型。在基于消费的资产定价模型中，假设股票的未来收益为、股票的当前价格为Pt、代表性个人的禀赋序列为｛et｝、代表性个人的效用函数为Ut（ct，ct+1）=u（ct）+βEt［u（ct+1）］，其中β为主观贴现率。由此，代表性个人的最优化问题为：

由此可解得代表性个人的最优化条件为

令股票收益率、随机贴现因子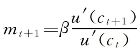^[58]，基于消费的资产定价模型可表示为：

引入无风险利率Rf后，有1=Et［mt+1］·Rf，式（3.8）又可表示为：

基于消费的资产定价模型则可表示为：

投资组合的风险溢价等于投资组合收益率对随机贴现因子的回归系数。然而，Mehra＆Prescott（1985^[59]）所提出的“股权溢价之谜”、Weil（1989^[60]）所提出的“无风险利率之谜”、Shiller（1981^[61]）所提出的“过度波动之谜”等，质疑了基于消费的资产定价模型。