在线求解进给速度优化问题的方法及优化

离线优化方法不能很好地适应真实的零件加工过程，而在线优化求解过程可以实时获取真实加工的实际工况，可根据加工过程当前的实际工况对工艺参数进行优化求解和反馈调控，这就有效地解决了离线优化无法准确预测工艺过程中各种因素的困难。

4.5.2.1　优化问题在线求解过程

铣削加工过程中，进给速度优化问题的在线求解本质上是实时确定零件加工刀位轨迹上每一点的铣削进给速度。进给速度优化问题的在线求解就是，根据当前的工况状态信息以及加工系统的输出响应实时计算确定下一时刻进给速度的过程。在求解的过程中，若要保证零件的加工时间最短，需要使零件加工刀位轨迹上每一点的铣削进给速度取得最大值，但是铣削进给速度的数值必须使得所有的约束条件都成立。

前面分析的优化约束准则中，并不是所有的约束条件都能在优化过程中起到约束作用。一系列的约束条件gi（f）≤0，i=1，2，…，7是冗余的，其中有一些约束条件是过于宽泛的，能够自然满足。由于机床、夹具等加工系统的刚度以及所能提供的加工能力一般远远超出工件-刀具子系统在加工过程中所能承受的范围，即加工过程中承受加工冲击的薄弱环节主要集中于工件-刀具子系统。因此，在求解参数优化问题过程中，可以舍弃机床进给速度约束、加工系统受力约束、铣削扭矩约束、铣削功率约束、切削速度约束等约束条件，只考虑与工件-刀具子系统相关的约束，即铣削力约束、刀具磨损速率约束。

铣削参数优化在线求解与调控本质上是控制学问题，即按照加工过程的最优目标及限制准则计算工艺参数的调控量。参数优化问题在线求解的过程为：根据实时监测得到的平均铣削力与刀具承受铣削力的限定值及时变工况对铣削力的影响计算进给速度的调整量；将计算获得的进给速度调整量累加到当前的进给速度上，得到新的进给速度；根据铣削过程中时变工况对刀具磨损速率的影响计算新的刀具磨损速率，验证优化得到的新进给速度是否满足刀具磨损速率的约束准则；如果满足，那么优化得到的新进给速度将作为下一时刻的进给速度；如果不满足，那么根据刀具磨损速率的约束准则重新计算新的进给速度，并将其作为下一时刻的进给速度。

铣削进给速度优化问题的在线求解步骤以及各个步骤间的数据流如图4.25所示。在线求解进给速度优化问题，得到最优化的铣削进给速度后，通过加工过程反馈控制模块对铣削加工过程进行反馈控制。

图4.25　进给速度优化在线求解步骤及各步骤间的数据流

上述流程为一个单次在线优化求解与实时反馈控制的过程。在真实的零件铣削加工过程中，会不断地对进给速度进行在线求解与反馈控制，往复循环以上过程，直至零件加工过程结束。

4.5.2.2　具体求解方法

1.铣削力获取

在真实的零件铣削加工过程中，一般通过切削力传感器在线测量X方向和Y方向的铣削力。当铣刀转角为φ时，测量的铣削力可以表示为矢量形式，其表达式为

式中：Fmeas（φ）是铣刀转角为φ时测量得到的OXY平面内的铣削力矢量。

OXY平面内的平均铣削力矢量可以通过计算测量的铣削力矢量在铣刀旋转一周范围内的平均值得到：

合力即为力矢量的模长。那么，加工过程中测量的铣刀所受的平均铣削力合力为测量的OXY平面内平均铣削力矢量的模长，其表达式为

2.平均铣削力合力与进给速度的关系

铣削加工过程中，平均铣削力矢量可以写成每齿进给量的线性形式，但平均铣削力的合力与每齿进给量之间不存在线性关系。因此，将平均铣削力的合力与每齿进给量的函数关系进行局部线性化，即一阶泰勒展开式。平均铣削力合力与每齿进给量的函数关系的一阶泰勒展开式为

式中：fz是铣削每齿进给量；fz，0是铣削加工过程中某一特定点的每齿进给量；||（fz）是平均铣削力的合力与每齿进给量的函数关系；||（fz，0）是铣削加工过程中某一特定点的平均铣削力合力；R1（fz）是一阶泰勒展开式的余项。

平均铣削力合力对铣削每齿进给量的一阶偏导数为

结合铣削力的计算公式，可以得到平均铣削力的合力与每齿进给量的函数关系的一阶泰勒展开式为

式中：Gc为平均剪切作用力的几何影响矩阵；K为剪切力系数矩阵。

3.计算优化进给速度

根据式（4.58）可知，平均铣削力合力与每齿进给量在局部成近似线性关系，即平均铣削力合力的增量与每齿进给量的增量近似成正比：

在计算优化的每齿进给量时，可以利用这一比例关系，通过实际测量的径向平均铣削力合力与其限定值的差值计算每齿进给量的调整值，即

式中：δfz是每齿进给量的调整量；Flim是已经设定的铣刀能承受的径向力的极限值；是径向平均铣削力合力，是通过在线测量与实时计算得到的；kp是每齿进给调整量比例系数，是k的倒数。

在铣削进给速度优化问题的在线求解过程（见图4.25）中，铣削力对比就是计算径向平均铣削力与其极限值的差值，即。

根据测量计算得到的径向平均铣削力，得到在线求解过程中的每齿进给调整量比例系数kp，其表达式为(www.xing528.com)

每齿进给调整量比例系数kp不仅与径向平均铣削力有关，还与平均剪切作用力的几何影响矩阵Gc、剪切力系数矩阵K相关。平均剪切作用力的几何影响矩阵Gc与刀具参数、铣削啮合形式等定常工况因素有关，还受到工艺参数等时变工况因素的影响。剪切力系数矩阵K与刀具涂层、工件材料等定常工况因素有关。

在计算每齿进给调整量比例系数kp时，式中的径向平均铣削力及其合力是通过在线测量与实时计算获得的（图4.25中铣削力获取）；平均剪切作用力的几何影响矩阵Gc和剪切力系数矩阵K需要根据当前实际加工过程的定常工况在工艺知识库中匹配获取；同时，平均剪切作用力的几何影响矩阵Gc的确定还需要考虑当前加工状态的时变工况，时变工况通过侦测加工获取（图4.25中过程侦测）。

得到径向平均铣削力与其极限值的差值，及每齿进给调整量比例系数kp后，可以通过式（4.60）计算每齿进给量的调整值。获得每齿进给量的调整值后，就可以计算优化后新的铣削进给速度了。

优化后新的每齿进给量可以通过在当前的每齿进给量上叠加每齿进给量调整值得到：

式中：是优化后新的每齿进给量；是当前实际的每齿进给量。

当前实际的每齿进给量可以通过当前实际的铣削进给速度及主轴转速计算得到：

式中：fcrt是当前实际的铣削进给速度；ncrt是当前实际的主轴转速；N是铣刀的齿数，在加工过程之前已经确定，加工过程中保持不变。将式（4.63）代入式（4.62）中，就可得到优化后新的每齿进给量。

优化后新的进给速度可以通过优化后新的每齿进给量与主轴转速计算得到：

当前实际的铣削进给速度及主轴转速为时变工况因素，由图4.25中的过程侦测获取。

4.验证刀具磨损速率约束准则

在该铣削进给速度优化问题中，除了刀具所受的径向平均铣削合力的约束准则外，还有另一个约束准则，即刀具磨损速率约束准则。根据第一个约束准则计算得到优化后新的铣削进给速度后，还需要根据第二个约束准则对其进行验证。

刀具磨损速率定义为单位切削加工时间内刀具后刀面磨损的增加量，即刀具后刀面磨损量对加工时间的导数。

式中：rVB是刀具磨损速率；VB是铣刀后刀面磨损量；t是加工时间。

刀具磨损速率可以表示成时变工况因素的函数：

式中：fz是铣削每齿进给量；vc是铣削切削速度。

将优化后新的每齿进给量，以及当前的铣削切削速度、后刀面磨损量代入式（4.66）中可以计算出与其相对应的刀具磨损速率。优化后新的每齿进给量可以通过优化后新的铣削进给速度及当前的主轴转速计算得到。当前的切削速度可以通过当前的铣削主轴转速和铣刀半径计算得到。

通过式（4.66）计算得到与优化后新的铣削进给速度相对应的刀具磨损速率，将其代入式（4.46）中，验证该刀具磨损速率是否满足该式的约束。如果式（4.46）的约束成立，则该磨损速率能够满足约束。那么，将其作为优化的结果。如果式（4.46）的约束不成立，则该磨损速率不满足约束。那么，需要根据刀具磨损速率约束准则重新计算铣削进给速度的优化结果。

5.重新计算铣削进给速度

如果优化后新的铣削进给速度不能满足刀具磨损速率约束准则，则需要根据刀具磨损速率约束准则重新计算铣削进给速度的优化结果，即寻找能够满足刀具磨损速率约束准则的最大铣削进给速度。

采用单点弦割法，对刀具磨损速率约束准则对应的方程进行求解，计算满足条件的铣削进给速度。将铣削加工过程中当前的每齿进给量作为单点弦割法的初始点，即固定的求解迭代点，将根据铣削力约束准则优化得到的每齿进给量作为单点弦割法的第一个迭代点，则可以表示为

在单点弦割法中，通过第j个解迭代计算第j+1个解的过程为，用初始固定点与第j个解的对应点之间连接的弦割线代替原来的方程表达式进行线性求解，以该直线的根作为迭代法中的第j+1个解。该求解过程的迭代公式为

式中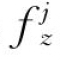：是单点弦割法中的第j个解；是单点弦割法中的第j+1个解。

在迭代求解停止的判定中，除了控制结果的精度外，还要确保求解的每齿进给量满足刀具磨损速率约束准则。迭代求解得到每齿进给量后，结合当前实际的铣削主轴转速计算与之相对应的铣削进给速度。

刀具磨损速率与每齿进给量的函数为增函数，重新计算得到的铣削进给速度要小于根据铣削力约束准则计算得到的铣削进给速度。因此，不需要再验证平均铣削合力的约束准则，即重新计算得到的结果为铣削进给速度优化的最终结果。

根据验证刀具磨损速率约束准则的结果，决定进给速度优化结果。优化结果将从根据铣削力约束准则计算的进给速度和根据刀具磨损速率约束准则计算的进给速度中选取。确定最终的铣削进给速度优化结果后，将其从优化求解流程中输出给进给速度反馈控制模块，同时将其记录于存储介质中，为铣削进给速度的离线学习提供数据基础。