薄壁零件误差补偿模型的优化求解

误差补偿的目的是将加工误差减小到精度范围内。对数学模型而言，求解误差补偿是计算令e=0时x的取值，即e（x）的零点计算问题。结合之前的分析，误差补偿的计算可以表示为而针对上述公式中不同的项取不同的值，有四种不同的零点迭代计算方法：镜像补偿法、牛顿（Newton）迭代法、前一点割线法、初始点割线法。

4.3.3.1　镜像补偿法

无论是采用误差预测法还是误差测量法，在计算补偿量时大都考虑镜像补偿法，即按照某个名义切深加工后产生的误差，都会以相同的量添加至下次加工的名义切深中，表示为

由式（4.8）可知，加工过程中的名义切深与实际切深的关系无论是线性的还是非线性的，都可以通过一系列迭代加工来减小误差。也正是这一方法的简单适用性，使其可应用于各种误差补偿场景。镜像补偿法的迭代效果可以通过补偿系数证明，其迭代过程如图4.9所示。可以看出，其收敛速度较慢。

图4.9　镜像补偿法迭代过程

4.3.3.2　牛顿迭代法

牛顿迭代法是求解非线性方程根的近似值的一种重要数值方法，其基本思想是利用非线性方程中的线性部分逐步逼近近似值。迭代过程可以表示为

牛顿迭代法具有2阶收敛速度，迭代过程如图4.10所示。

4.3.3.3　前一点割线法

牛顿迭代法每次迭代计算时都需要计算加工过程f的一阶导数值。由于f的复杂性，名义切深与实际切深之间的关系很难确定，这也是使用迭代法求解该误差模型的原因。然而这一复杂关系导致了f的一阶导数值很难计算，使得牛顿迭代法只能作为数学原理表示。为了避免计算导数，改用平均变化率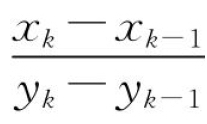替代牛顿迭代公式中的，则式（4.9）变为如下形式：

图4.10　牛顿迭代法补偿迭代过程

在计算每一步的平均变化率时都需要前两步的信息（xk，yk）和（xk-1，yk-1），这种迭代法为两步法。当k=0时，令xk1=yk1=0。

采用这种用平均变化率替代导数的方法，迭代的几何意义从切线法变为割线法。更具体的是，平均变化率使用的是当前点与前一点的割线，因此该方法称为前一点割线法。前一点割线法具有1.618阶收敛速度，迭代过程如图4.11所示。

图4.11　前一点割线法补偿迭代过程(www.xing528.com)

4.3.3.4　初始点割线法

前述的迭代公式构建方法都是从非线性方程零点计算角度进行的。结合薄壁零件加工弹性变形原理，可以从物理和几何角度对误差进行控制。在此基础上，引入回弹系数λ的概念，表示变形量与名义切深的商，即

对于ε，有

其中，zi为第i次加工名义切深与第i-1次加工名义切深的差值。

如图4.12所示，当k=0即未补偿加工时，名义切深为x0，加工误差为e0，回弹系数为

图4.12　未补偿加工时各参数的关系

在假设当前刚度与切削力不变的情况下，利用回弹系数，计算令误差为0的下次加工，即第一次补偿加工时的名义切深x1，有如下关系：

当第k次补偿加工时，名义切深为xk，加工误差为ek，以此计算回弹系数λk，并在假设当前刚度与切削力不变的情况下，计算令误差为0的第k+1次补偿加工的名义切深xk+1，如图4.13所示，有如下关系：

图4.13　第k次补偿加工后各参数的关系

经过变形，得到误差补偿公式

初始点割线法的迭代过程如图4.14所示，具有1阶收敛速度，低于前一点割线法。

图4.14　初始点割线法补偿迭代过程