考虑振动条件的切削力预测模型优化

3.5.1.1　理想条件下的切削力模型

首先，不考虑刀具的偏心、倾斜等条件，以传统方法将刀具沿轴向离散为多个微元，每个微元长度为dl。同时，将坐标系建立在刀具上，此坐标系是不同于机床坐标系的刀具坐标系OcXcYcZc，切削力的预测将在这个坐标系内完成。Xc是刀具进给方向，Zc是刀具轴向。在加工过程中，每个微元都进行斜角切削。如图3.6所示，每个微元的切削力被分解为切向力Ft、径向力Fr和轴向力Fa：

图3.6　单一微元上的切削力

式中：Ktc、Krc、Kac为剪切力系数；Kte、Kre、Kae为刃口力系数；h（φ）为瞬时未变形切屑厚度（IUCT），可以用带有每齿进给量fz的公式近似表示，即

将切削力转换到刀具坐标系中，整理得到

在某一时刻t，一条切削刃与工件接触产生的力是由刀刃上所有微元所产生的，因而沿刀具轴向高度上积分即可获得一条刀刃上的切削力。经过换元积分得到

式中：φ2和φ1是积分上下界，且由于刀刃的实际接触状态随着刀具的转动而变化，需要进行判断。用l1表示积分开始的点距离刀具底部的高度，l2表示积分结束的点距离刀具底部的高度（l1≥0，l2≤ap）。对切削而言，存在以下关系：刀刃与工件未接触时，l1=0，l2=0，则φ1=0，φ2=0；刀刃与工件接触时，如图3.7所示，分为两种情况［8］。

图3.7　刀具接触情况

（1）如果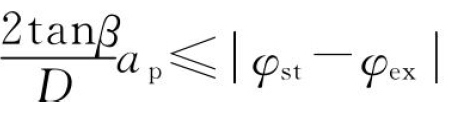，则

①当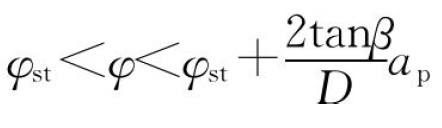时，l1=0，l2≠0且l2≠ap，则；

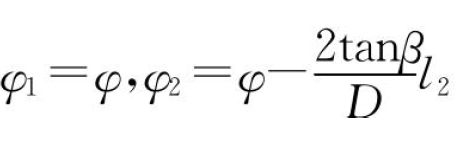②当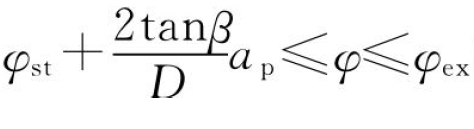时，l1=0，l2=ap，则；

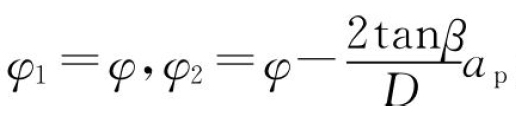③当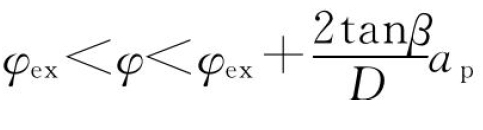时，l1≠0，l2≠0，则。

（2）如果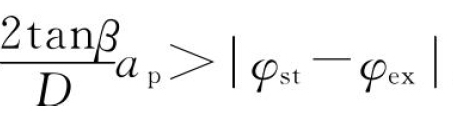，则

①当φst＜φ＜φex时，l1=0，l2≠0且l2≠ap，则；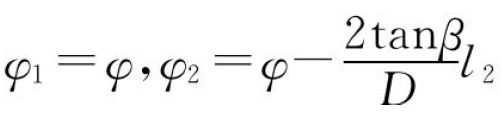

②当时，l1≠0，l2≠0，则φ1=φex，φ2=φst；

③当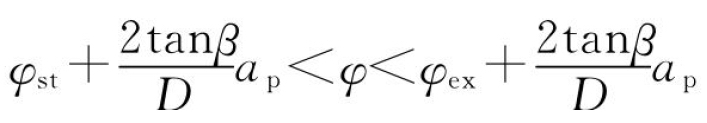时，l1≠0，l2=ap，则φ1=φex，φ2=φ-。

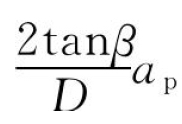结合sign函数，可以得到以下公式：

其中，l1、l2的值可以由刀具-工件的几何接触算法给出，这时最终获得的φ1、φ2与刀具的位置角φ没有关系。因而，这个公式可以用于除槽铣以外的加工，此时l1、l2的值是时间的函数，也就可以得到以下公式：

这里的计算需要接触算法离散地给出多个时间点t1，t2，…，tn上l1（t）和l2（t）的值，这些值组成了一个矩阵L。如果有多个刀刃，则需要多个矩阵，从而可以写出一个特定刀刃i的切削力：

当多个刀刃都有接触的时候，切削力可以表示为

3.5.1.2　振动条件下的未变形切屑厚度与切削力模型

实际加工过程中，由于刀具-主轴子系统刚度有限，刀具振动带来的动态位移不可避免。真实的刀具 主轴子系统可以看成一个包含多个截面、形状多变的复杂梁系统，该系统受到复杂支撑条件（轴承和机床结构）约束，其内部各个部分间的耦合关系也对子系统整体的动力学特性有明显影响。该系统在实际加工过程中受到的动力学激励为刀具端部受到的切削力。由于系统刚度有限，并且系统的内部组成关系和边界条件较为复杂，因此全系统的振动是在空间和时间中的连续过程。理论上在切削过程中，刀具-主轴子系统整体作为一个连续系统在切削力的作用下振动，但除刀具端部与工件接触区域的振动会在工件表面产生波纹并影响切削力的产生外，全系统其他部分的振动情况对切削过程的影响可以忽略。因此，可以将整个连续振动系统等效简化为一个由刀具端部构成的点振动系统。同时刀具-主轴子系统在垂直方向有极大的刚度，但沿刀具轴向、Zc方向的振动可以忽略不计。以多步等效简化为基础，连续的刀具-主轴子系统可以被简化为一个二自由度（2-DOF）的振动系统，如图3.8所示。在刀具坐标系内，这一二自由度系统的振动可以用一组微分方程来表示：

式中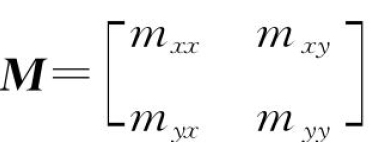：，为模态质量矩阵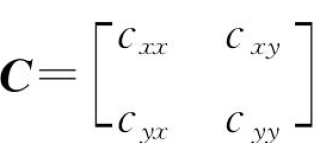，为模态阻尼矩阵；K=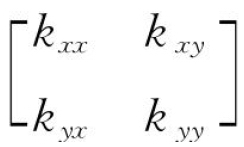，为模态刚度矩阵。(www.xing528.com)

忽略x方向和y方向的耦合作用，即一个方向的激励在另一个方向的影响，该系统可以表示为

图3.8　刀具子系统动力学模型与动态切屑厚度

式中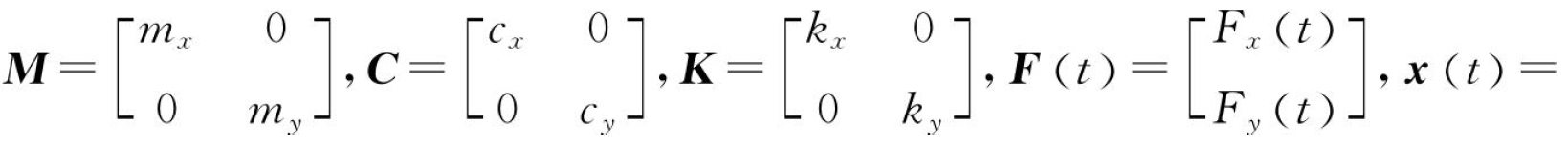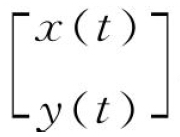：。式中除力和位移以外的系统动力学参数可以通过模态实验获得。

刀具振动导致了刀具位置的变化，改变了刀具切削过程中的未变形切屑厚度，从而导致了切削力的动态变化。在图3.8中，无振动条件下刀具切削产生的新加工表面即为黑色实线，无振动条件下刀具的负载由准静态未变形切屑厚度决定，用hs，i，j（φi，j（t），κi，j）表示。当刀具正在振动的时候，切削刃会使新加工的表面变成波纹状。加工过程中的未变形切屑厚度不仅仅受到刀具瞬时振动位移的影响，而且也受到前一切削刃在切削上表面遗留波纹的影响。为了能够将刀具振动的影响在切削力的计算中表现出来，可以在理论每齿进给量上附加一个动态进给量：

式中：T为连续两个刀齿切入的时间差，，其中，φp为刀具相邻两齿之间的齿间角。x（t）和y（t）分别为刀具在x和y方向的振动位移。

另外一个需要考虑的情况是，当振动的幅度达到一定值，超过了理论每齿进给量时，刀具会脱离工件，而未切除的材料会直接增加下一个刀齿的切削负载。更加极端的情况是，有多个刀齿因振动连续脱离工件，那么附加进给量就与上一个切入的刀齿所在的位置相关，这个位置可以表示为

这样，产生未变形切屑厚度动态变化的附加进给量可以表示为

式（3.52）中的fv实现了考虑刀齿连续切入的时滞耦合效应，同时消除了刀具振动方程中的时滞耦合项。最终，在第i个刀齿的第j个微元上的动态未变形切屑厚度为

式中：κi，j为轴向浸入角。

记dsi，j为刀具第i个刀齿的第j个微元的长度，dbi，j为刀具第i个刀齿的第j个微元的切屑厚度，根据动态未变形切屑厚度，微元切削力可以写成如下形式：

其中，Hi，j（t）为作用在前刀面上的真实未变形切屑厚度。作用在整个刀具上的切削力为所有切入微元上切削力的和：

由于振动和切削力的耦合效应，预测流程是一个非线性的过程，其中系统动力学方程的求解可以通过经典四阶龙格-库塔（Runge-Kutta）法完成，并设初值为0（包括速度和位移的初值）。同时，仿真过程中使用的时间步长和实验过程中由采样频率确定的时间步长一致。预测的基本流程如下：

（1）在每一个时间点tk，同时计算确定刀具的转动角度φ、切入微元的个数M以及每个微元的切入角φj，st（tk）和切出角φj，ex（tk）；

（2）与此同时，获得相对于现在时间点的前一个刀具从工件切除材料的位置xP（tk）；

（3）获得刀具微元的位置角度φi，j（tk）并判断微元切入与否的g（φi，j（tk））后，计算当前刀具位置x（tk）和每一个微元上的切削力Ft，i，j（tk）、Fr，i，j（tk）、Fa，i，j（tk）；

（4）存储实时的切削力Fx（tk）、Fy（tk）、Fz（tk）和刀具振动位移x（tk）、y（tk）及速度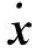（tk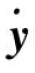）、（tk），用于后面的计算；

（5）如果所有的预测计算时间步均计算完成，算法终止并输出结果；否则，跳回第（1）步。

与传统计算方法中简单地将每个微元上的力相加不同，这个计算流程必不可少的环节为伴随切削力的计算求解刀具的振动（第（4）步）。在求解每一个刀具微元切削力之前，前面一个刀具切入工件的位置需要从存储的数据中筛选出来（第（2）步）。

当轴向切深ap足够小（根据经验，一般为1～2 mm）时，ap可以约等于一个刀具微元的长度dz，同时，ae也足够保证在任何时刻只有一个刀刃与工件接触。这种状态在加工钛合金和高温合金的时候相对比较常见。此时，切削力模型可以简化为

式中：

此时，接触计算只要给出切入角φst、切出角φex和接触刀齿的位置角度φ即可：当φst≤φ≤φex时，δ=1；否则，δ=0。