企业股票估价方法及重要因素解析

股票的估价就是计算股票的价值，然后与股票市价作比较，视其低于、等于、高于市价来决定是买入、卖出还是继续持有。股票的价值由其未来现金流量贴现所决定，所用的贴现率按投资人要求的必要报酬率进行贴现（见图6-1）。与债券现金流量不同，股票现金流量有更大的不确定性。

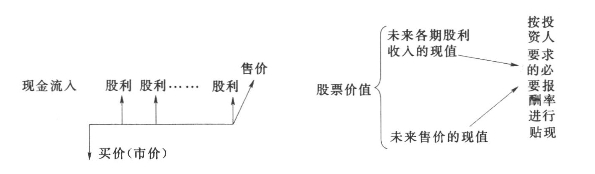
图6-1　股票价值构成

【例6-2】　估算股票价值时的贴现率，不能使用（　）。

A.股票市场的平均报酬率

B.债券收益率加适当的风险报酬率

C.国债的利息率

D.投资人要求的必要报酬率

解析：股票价值是指未来现金流入的现值，折现时应以投资人要求的必要报酬率为贴现率，而股票投资有风险，投资人要求的必要报酬率必然高于国债的利息率，所以不能用国债的利息率作为估算股票价值时的贴现率。故答案是C

（一）股票评价的基本模型

股票未来的现金流量有两类：一是支付的股利，二是出售股票时的售价。所以，股票的价值基本模型公式如下：

式中　V——股票的购买价格；

Vn——股票的出售价格；

Dt——股票投资的报酬（第t年获的股利）；

K——投资收益率；

n——投资期限。

可以说，股票内在价值是等于下一期股利和下一期股票出售价格的现值总和。或者说股票内在价值是等于以后所有各期股利的现值。我们通过实践证明一下：

例如某人持有股票1年，为得到股票其支付的价格为V0，得求第一个公式：

式中　D1——第一年末收到的股利；

P1——第一年末股票的出售价格（投资者第一年末购买股票支付的价格）；

V0——股票投资的现值（股票内在价值）；

K——贴现率。

第一年末股票投资者决定股票内在价值的方法为V1，得出第二个公式：

式中　D2——第二年末的股利；

P2——第二年末股票的出售价格。

将第二个公式代入第一个公式，则有：

以此类推，则有：

由此可见，以上关于股票内在价值计算的两种观点都是正确的。

即，股票内在价值是等于下一期股利和下一期股票出售价格的现值总和；也等于以后所有各期股利的现值。

因此，上式可以认为是股票估价的一般模型。用其计算股票内在价值时，通常假设公司在未来某个时候支付股利，当公司清算或被并购时，也会因支付清算股利或回购股票而发生现金支付。若公司从不支付任何现金股利或其他形式的股利，则股票价值等于零。

（二）几种常见的股票评价模型

1.零成长股票估价模型

这种股票的估价方法的使用有两个前提：(www.xing528.com)

（1）企业一旦购入普通股，将长期持有。

（2）股票投资的股利收入金额在若干年内保持不变。

在这两个前提下，股票的内在价值是普通股未来股利按投资者的收益率折成现值的总称。即：

由于每年发放固定的股利，即D1=D2=D3=…=D，而且企业准备长期持有该股票，则n→∞，那么，零成长股票股价模型为：

式中　V——股票的内在价值；

D——一年内的股票股利；

K——企业预期的收益率。

【例6-3】2006年，某公司每股普通股的年股利额为8.9元，企业投资要求得到的收益率为13%，则普通股的内在价值为：

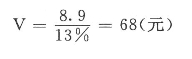
如果企业投资于这种股票的收益率不低于13%，股票的购入价格就不得高于68元，否则就不适宜这项投资。

2.固定成长股票的估价模型

固定成长股票的估价也有两个假设条件：

（1）股利按固定的年增长率增长，该增长率用g表示。

（2）股利增长率总是低于企业期望的收益率。

股票的内在价值也是普通股未来股利按投资者的收益率折成现值的总称。如图6-2所示。

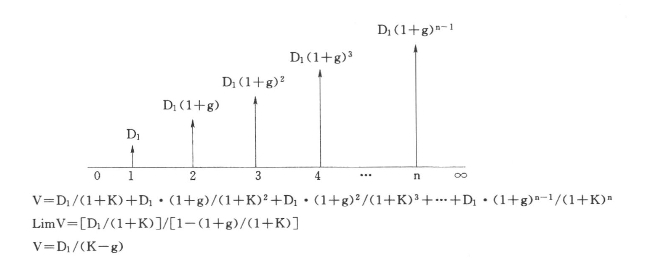
图6-2　固定成长股票股价模型图

需要注意的问题：①公式的通用性；②区分D和D0；③K的确定。

设：固定成长股票股利以固定的比例g增长，则未来第t期的预期股利Dt=D0（1+g）t，根据股票估价一般模型则有：

假设K＞g（这是个很合理的假设，因为若K＜g，则股票价值为无穷大），上式可简化为：

式中　D1——未来第一期的股利。

上式经变化后可求出投资者要求的报酬率

【例6-4】2006年，某公司普通股基年股利D0为4元，估计每年增长率为3%，企业投资要求得到的收益率为12%，求该普通股的内在价值？

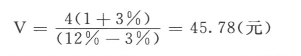
【例6-5】　某种股票当前的市场价格是40元，每股股利是2元，预期的股利增长率是5%，则由市场决定的预期收益率为（　）。

A.5%　B.5.5%　C.10%　D.10.25%

K=D1/V+g=2×（1+5%）/40+5%=10.25%

所以答案为D

【例6-6】　某投资人准备投资于A公司的股票，A公司没有发放优先股，20××年的有关数据如下：每股账面价值为10元，每股盈余为1元，每股股利为0.4元，该公司预计未来不增发股票，并且保持经营效率和财务政策不变，则，可持续增长率为6.38%。现行A股票市价为15元，目前国库券利率为4%，证券市场平均收益率为9%，A股票β系数为0.98。经计算，A股票投资的必要报酬率为8.9%。

要求：问该投资人是否应以当时市价购入A股票？

A股票的价值为：

由于股票价值高于市价，所以可以以当前市价购入。