资金时间价值计算的两种方法及实例分析

（一）一次性收付款项现值与终值的计算

一次性收付款项资金时间价值的计算有单利制和复利制两种计算方法。

1.单利制

单利方式计算利息的原则是本金按年数计算利息，而以前年度本金产生的利息不再计算利息。因而，在单利计算方式下，资金现值与终值的计算比较简单。

按照单利的计算法则，利息的计算公式为

I=p·i·n

式中　i——每一计息期的利率（折现率），通常指每年利息与本金之比；

I——利息；

p——本金，又称期初额或现值；

n——计算利息的期数。

每年的利息额就是资金的增值额，资金的终值就是本金与每年的利息额之和。

（1）单利终值的计算公式为

Fn=p+I=p+p·i·n=p（1+i·n）

式中　Fn（或者F）——本金与利息之和，又称本利和或终值。

（2）单利现值的计算是终值计算的逆运算，计算公式为

p=Fn/（1+i·n）=Fn-I

【例2-1】　某企业有一张带息期票，面额为2400元，票面利率为8%，出票日期6月15日，8月14日到期（共60天），则到期时利息为：

I=2400×8%×60/360=32元

2.复利制

资金的时间价值一般都是按复利方式进行计算。所谓复利制，是指每经过一个计息期，要将所生利息加入本金再计利息，逐期滚算，俗称“利滚利”。复利不同于单利，既涉及本金的利息，也涉及以前年度的利息继续按利率生息的问题。

（1）复利终值的计算（已知现值p，求终值Fn）。复利终值是指若干期以后包括本金和复利利息在内的未来价值。复利终值的一般计算公式为：

Fn=P（1+i）n

式中　Fn——复利终值；

P——复利现值；

i——利息率；

n——计息期数。

其中，（1+i）n称作“复利终值系数”，记作（F/p，i，n），可以通过查阅“一元复利终值表”直接获得。因而，复利终值的计算可以转化为本金与系数乘积的形式。即：

Fn=P（F/p，i，n）

【例2-2】　将10000元存入银行，利息率为10%，要求：计算5年后应从银行取得多少钱？

或者：F5=P（F/p，i，n）=10000×（F/p，10%，5）

查表可得：（F/p，10%，5）=1.611，则，

（2）复利现值的计算（已知终值Fn，求现值p）。复利现值是指以后年份收入或支出资金的现在价值。由终值求现值，叫做贴现。在贴现时所用的利息率叫贴现率。

实际上计算复利现值是计算复利终值的逆运算，按折现率i计算的复利现值为：

p=Fn（1+i）-n

其中，（1+i）-n称作“复利现值系数”，记作（p/F，i，n），可以通过查阅“一元复利现值表”得到。复利现值的计算可以转化为将来值与系数乘积的形式。即

p=Fn（p/F，i，n）

【例2-3】　若计划在3年以后得到10000元，利息率为8%，要求：计算现在应存金额多少钱？

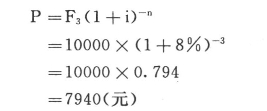
或者：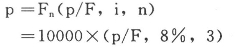

查表可得：（F/p，8%，3）=0.794，则

（3）复利利息的计算公式。

I=Fn-P

（4）名义利率与实际利率。上述计算均假定利率为年利率，每年复利一次。但实际上，复利的计息期间不一定总是一年，有可能是季度、月份或日。比如某些债券半年计息一次，有的抵押贷款每月计息一次，银行之间拆借资金均为每天计息一次。当每年复利次数超过一次时，给出的年利率叫做名义利率，而每年只复利一次的利率叫做实际利率。

【例2-4】　本金10000元，投资5年，利率8%，每年复利一次，其本利和与复利息：

F5=10000×（1+8%）5=10000×1.469=14690（元）

I=14690-10000=4690（元）

如果每季复利一次，每季度利率=8%/4=2%；复利次数=5×4=20。

F20=10000×（1+2%）20=10000×1.486=14860（元）

I=14860-10000=4860（元）

当一年内复利几次时，实际得到的利息要比按名义利率计算的利息高。【例2-4】中实际利率为：

Fn=P（1+i）n

14860=10000×（1+i）5

（1+i）5=1.486

即　（F/p，i，n）=1.486

查表得：　（F/P，8%，5）=1.469，（F/P，9%，5）=1.538

用插补法求得实际利率：

对于一年多次复利的情况，可采取两种方法计算资金的时间价值。

1）按计算公式把名义利率调整为实际利率，然后按实际利率计算时间价值。公式为：

i=（1+r/m）m-1

式中　r——名义利率；

m——每年复利次数；

i——实际利率。

2）不计算实际利率，而是相应调整有关指标，即利率变为r/m，期数相应变为m·n。

（二）年金终值与现值的计算（非一次性收付款项终值与现值的计算）

年金是指在一定时期内每次等额的收付款项。例如，分期付款赊购，分期偿还贷款，发放养老金，分期支付工程款，每年相同的销售收入等，都属于年金收付形式。年金按其收付发生的时点不同，可分为普通年金、即付年金、递延年金，永续年金。不同种类年金的计算用以下不同的方法计算。年金一般用符号A表示。

1.普通年金的计算

普通年金是指一定时期内每期期末等额收付的系列款项，又称后付年金。普通年金的计算有普通年金终值的计算和和普通年金现值之分。

（1）普通年金终值的计算（已知年金A，求年金终值FA）。

普通年金终值犹如零存整取的本利和，它是一定时期内每期期末等额收付款项的复利终值之和。普通年金终值一般用符号FA表示。普通年金终值的计算公式为：

FA=A（1+i）0+A（1+i）1+A（1+i）2+…+A（1+i）n-1

整理上式，可得到：FA=A［（1+i）n-1］/i，式中的分式称作“年金终值系数”，记作（F/A，i，n），可以通过直接查阅“1元年金终值系数表”求得有关数值。上式可以记作：

FA=A（F/A，i，n）

式中　A——年金数额；

i——利息率；

n——计息期数；

FA——年金终值。

普通年金终值的计算见图2-1。

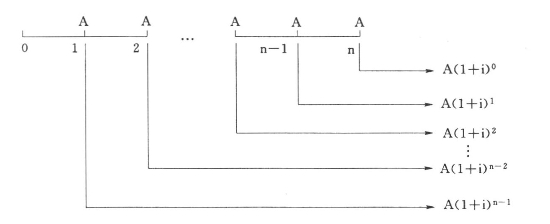
图2-1　普通年金的终值

【例2-5】5年中每年年底存入银行10000元，存款利率为8%，求第5年末年金终值为多少？

（2）普通年金现值的计算（已知年金A，求年金现值PA）。

普通年金现值是指一定时期内每期期末收付款项的复利现值之和，整存零取求最初应存入的资金额就是典型的求普通年金现值的例子。普通年金现值的符号一般用PA表示。

普通年金现值计算见图2-2。

图2-2　普通年金的现值

普通年金现值的计算公式为：(www.xing528.com)

［1-（1+i）-n］/i称作“年金现值系数”，可以通过查阅“1元年金现值系数表”直接获得。所以，计算公式也可以写为：

PA=A（P/A，i，n）

【例2-6】　张华现在存入一笔钱，准备在以后5年中每年末得到10000元，如果利息率为10%，要求：计算张华现在应在银行存入多少钱？

（3）偿债基金的计算（已知年金终值FA，求年金A）。

偿债基金是指为了在约定的未来时点清偿某笔债务或积蓄一定数量的资金而必须分次等额形成的存款准备金。由于每次提取的等额准备金类似年金存款，因而同样可以获得按复利计算的利息，所以债务实际上等于年金终值。计算公式为：

A=FA·i/［（1+i）n-1］

i/［（1+i）n-1］称作“偿债基金系数”。偿债基金系数是年金终值系数的倒数，可以通过查“一元年金终值表”求倒数直接获得，所以计算公式也可以写为：

A=FA（A/F，i，n）=FA/（F/A，i，n）

【例2-7】　杨林拟在5年后还清100000元债务，从现在起每年等额存入银行一笔款项，假设银行存款利率10%，试问：杨林每年需要存入多少元，5年后才能还清100000元债务？

A=100000/（F/A，10%，5）=100000/6.105=100000×0.1638=16380（元）

（4）资本回收额的计算（已知年金现值PA，求年金A）。

资本回收是指在给定的年限内等额回收或清偿所欠的债务（或初始投入资本）。年资本回收额的计算是年金现值的逆运算。其计算公式为：

A=PAi/［1-（1+i）-n］

i/［1-（1+i）-n］称作“资本回收系数”，记作（A/P，i，n）。资本回收系数是年金现值系数的倒数，可以通过查阅“一元年金现值表”，利用年金现值系数的倒数求得。所以计算公式也可以写为：

A=PA（A/P，i，n）=PA/（P/A，i，n）

【例2-8】　假设谭玲以10%的利率借得20000元，投资于某个寿命为10年的项目，每年至少要收回多少现金才是有利的？

2.预付年金的计算

预付年金是指在一定时期内，各期期初等额的系列收付款项，又称即付年金或先付年金。

预付年金与普通年金的区别仅在于付款时间的不同。利用普通年金系数表计算预付年金的终值和现值时，可在普通年金的基础上用终值和现值的计算公式进行调整。

（1）预付年金终值的计算。

预付年金终值公式推导过程：

FA=A（1+i）1+A（1+i）2+…+A（1+i）n

根据等比数列求和公式可得下式：

FA=A｛［（1+i）n+1-1］/i-1｝

其中，｛［（1+i）n+1-1］/i-1｝是预付年金终值系数，或称1元的预付年金终值，它和普通年金终值系数［（1+i）n-1］/i相比，期数加1，而系数减1，可记作［（F/A，i，n+1）-1］。

或者，FA=A（1+i）1+A（1+i）2+…+A（1+i）n中右端提出公因子（1+i），可得下式：

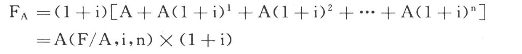
因此预付年金终值的计算公式为：

［（F/A，i，n+1）-1］或A（F/A，i，n）×（1+i）

预付年金终值的计算见图2-3。

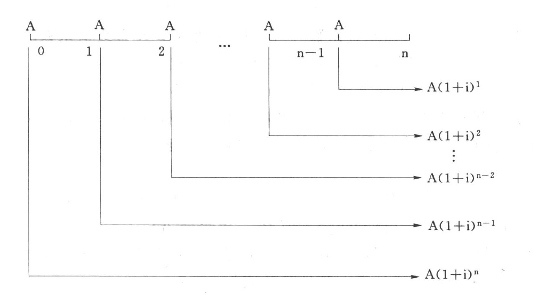
图2-3　预付年金终值

【例2-9】　某人每年年初存入银行10000元，银行存款年利率为8%，问此人第10年末的本利和应为多少？

（2）预付年金现值的计算。

我们同样用普通年金现值公式来推导：

从图2-4可知，预付年金现值由于第一期期初数不需要贴现，因而比普通年金少一期，即假设普通年金为n期，则先年付年金为n—1期，因此，预付年金现值公式为：

PA=A+A（1+i）-1+A（1+i）-2+…+A（1+i）-（n-1）

根据等比数列求和公式可得下式：

PA=A｛［1-（1+i）-（n-1）］/i+1｝

其中，｛［1-（1+i%）-（n-1）］/i+1｝是预付年金现值系数，或称1元的预付年金现值，它和普通年金现值系数［1-（1+i%）-n］/i相比，期数要减1，而系数要加1，可记作：［（P/A，i，n-1）+1］。

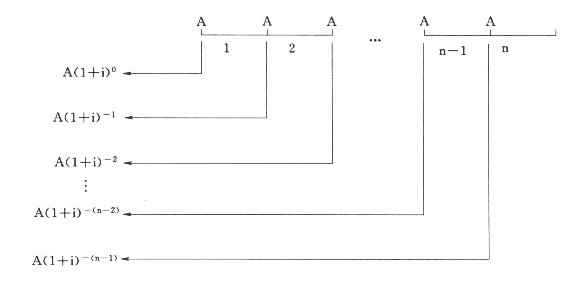
图2-4　预付年金现值

或者，PA=A+A（1+i）-1+A（1+i）-2+…+A（1+i）-（n-1）中两端同乘以（1+i），得：

（1+i）PA=A（1+i）+A+A（1+i）-1+…+A（1+i）-（n-2）

再与原式相减，得：

i·P=A（1+i）-A（1+i）-（n-1）

PA=A［1-（1+i）-n］/i（1+i）

【例2-10】6年分期付款购物，每年初付2000元，设银行利率为10%，该项分期付款相当于一次现金支付的购价是多少？

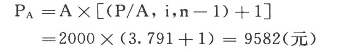
【课堂练习题】　某企业租用一设备，在10年中每年年初要支付租金5000元，年利息率为8%，问这些租金的现值是多少？

3.递延年金的计算

递延年金是指第一次收付款发生时间与第一期无关，而是隔若干期（假设为m期，m≥1）后才开始发生的系列等额收付款项。它是普通年金的特殊形式，凡不是从第一期开始的普通年金就是递延年金。

假设最初有m期没有收付款项，后面n期有等额的收付款项，则延期年金的现值即为后n期年金贴现至m期第一期期初的现值。

递延年金现值的计算方法主要有以下两种：

（1）先求出（m+n）期后付年金现值，再减去没有付款的前m期后付年金现值，两者之差便是延期m期的n期后付年金现值。其计算公式为：

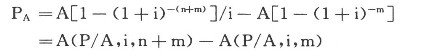
（2）将递延年金看成n期普通年金，先求出第m+1期期初时的n期普通年金的现值，然后再折算到第一期期初，即得到n期递延年金的现值。

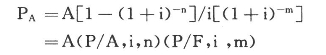
递延年金终值的计算与普通年金相同，前面没有发生收付款的时期不计算，后面发生收付款的时期有几期按期数和折现率计算终值。

【例2-11】　某企业向银行借入一笔款项，银行贷款的年利息率为8%，银行规定前10年不用还本付息，但从第11年至第20年每年年末偿还本息10000元，问这笔款项的现值应为多少？

或者

4.永续年金的计算

永续年金是指无限期等额收付的年金，可视为普通年金的特殊形式。无限期债券的利息和优先股的股利都是永续年金的例子。由于永续年金持续期无限，没有终止的时间，因此没有终值，只有现值。利率较高、持续期限较长的年金都可以视同永续年金计算。永续年金现值的计算公式可由普通年金现值的计算公式推算获取。

PA=A［1-（1+i）-n］/i

n→∞，（1+i）-n的极限为0。

PA=A/i

【例2-12】　某学校拟建立一项永久性的奖学金，每年计划颁发10000元奖金，若利率为10%，现应存入多少钱？

PA=10000/10%=100000（元）

【课堂练习题】　某永续年金每年年底的收入为8000元，利息率为8%，求该项永续年金的现值？

5.相关贴现率计算

（1）永续年金贴现率的推算。永续年金折现率的计算也很方便。若PA，A已知，则根据公式PA=A/i变形即得折现率的计算公式：i=A/PA

（2）普通年金贴现率的推算。普通年金贴现率的推算比较复杂，无法直接套用公式，必须利用有关的系数表，有时还要牵涉到内插法的运用。下面我们介绍一下计算的原理。

实际上，我们可以利用两点式直线方程来解决这一问题：

两点（X1，Y1），（X2，Y2）构成一条直线，则其方程为：

（X-X1）/（X2-X1）=（Y-Y1）/（Y2-Y1）

这种方法称为内插法，即在两点之间插入第三个点，于是对于知道n，i，F/p这三者中的任何两个就可以利用以上公式求出。

因此，普通年金折现率的推算要分两种情况分别计算，下面着重对此加以介绍。

1）利用系数表计算。根据年金终值与现值的计算公式：

FA=A（F/A，i，n）和P=A（P/A，i，n）

将上面两个公式变形可以得到下面普通年金终值系数和普通年金现值系数公式：

（F/A，i，n）=F/A，（P/A，i，n）=P/A

当已知FA，A，n或P，A，n，则可以通过查普通年金终值系数表（或普通年金现值系数表），找出系数值为FA·n/A的对应的i值（或找出系数值为P/A的对应的i值）。对于系数表中不能找到完全对应的i值时，可运用下面的试算内插法计算。

2）利用内插法计算。查表法可以计算出一部分情况下的普通年金的折算率，对于系数表中不能找到完全对应的i值时，利用年金系数公式求i值的基本原理和步骤是一致的，以已知P，A，n为例，说明求i值的基本方法。

若已知P，A，n，可按以下步骤推算i值：①计算出P/A的值，假设P/A=α；②查普通年金现值系数表。沿着已知n所在的行横向查找，若恰好能找到某一系数值等于α，则该系数值所在的行相对应的利率就是所求的i值；若无法找到恰好等于α的系数值，就应在表中n行上找到与α最接近的左右临界系数值，设为β1，β2（β1＞α＞β2，或β1＜α＜β2）。找出β1，β2所对应的临界利率，然后进一步运用内插法。