生产商净资产与最优筹资总量的决定要素

由上文可知，在银行局部最优均衡条件下，个体风险因子φM及未违约条件下的贷款利率为与市场平均资本回报率为，所需要筹集的资本总额，贷款数额等变量密切相关。下文将以此文基础，重点分析生产商所筹集资本的决定因素。

根据式5.4的约束条件，可进一步推导出生产商筹资的期望收益：

该式表明当生产商M面临的个体风险φM≥φM时，则厂商的净收益为。但当φM＜φM时，则生产商的收益则为零。

将式5.23写成期望的形式，则可得：

式5.24就是生产商筹资的期望收益，将银行的局部均衡最优均衡等式5.8代入，则可将式5.24转化为：

由此可见，生产商的期望收益YE与临界风险因子φM均为市场平均资本回报率的函数式。

设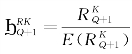，指实际资本回报与期望资本回报的比值，则式5.25可写为：

综合上文分析，式5.26描述了生产商在面临银行局部均衡等式约束时的期望收益选择。由于银行遵循风险厌恶的设定，由企业违约所承担的成本也包含在该式中。若将该式最大化，则可解得两个关键变量所需冲击资本数量和临界风险因子φM(由市场平均资本回报率的函数式表达)的关系，从而确定其他包括单位资本价格ZQ，净资产等变量的最优值。

由上文可知1-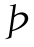(φM)为生产商筹资的期望收益比重，故其期望贷款收益又可写做，故最大化式5.26又可转化为以下形式进行详细讨论：

此处先设外源融资溢价，财务杠杆lQ=ZQ·，λ为拉格朗日乘数，则式5.27的一阶化条件为：

由式5.28，可得拉格朗日乘数λ为φM的函数，故：

对其求导：

上文已证明银行可获得的期望贷款收益比重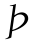(φM)-τ(φM)先增后减，在φM=φM*处取得最大值，故作为银行而言不会选择在φM＞φM*的阶段放贷。当φM∈(0，φM*)时，可知λ′(φM)恒大于零。继续对其取极限：

由上文推导表明随临界风险因子φM的增加，拉格朗日乘数函数λ(φM)也随之增加，区间为(1，+∞)。

由式5.29，可得：(www.xing528.com)

对该式求导：

同样基于上文假定，当φM∈(0，φM*)时，Ч′(φM)大于零，表明Ч(φM)在相应区间是增函数。对其求极限：

上文推导表明随着临界风险因子φM的增加，生产商的外部融资溢价epQ=Ч(φM)也呈现上升趋势。

由式5.30，可得：

对该式求导：

类似地，根据上文假定，当φM∈(0，φM*)时，大于零，表明在相应区间是增函数。对其求极限：

由上文推导表明随着临界风险因子φM的增加，生产商的财务杠杆lQ=也呈现上升趋势。

至此，临界风险因子φM，生产商的外部融资溢价epQ=Ч(φM)以及财务杠杆在φM∈(0，φM*)区间内的联动关系已呈现。当生产商面临风险增加时，企业的财务杠杆与外部融资溢价都会呈现出上升的趋势。

将上述关系整理可得lQ财务杠杆为外部融资溢价epQ的增函数，可得：

由上文所述，由于φM*是一个可取到的定值，故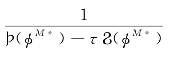也是如此，并非无限发散。

将式5.42继续整理：

，且

式5.43可视为生产商所筹资本总额的决定等式，详细描述了在本研究设定的局部均衡约束条件下，生产商所需要筹集的资本总额与其财务状况的关系。其中，生产商的财务状况用外部融资溢价以及净资产来共同表示。由于也是φM的函数，所以当所筹资本数量确定后，那么依据该等式及设定的约束条件，φM的值也将确定。换而言之，式5.43实际将以企业最优选择为核心的各个变量间的一一对应关系均予以展现。

从现实经济含义上分析，式5.43表明生产商所筹集的资本总额是随着企业净资产的上升而增加，这个幅度则由与市场平均资本回报率为及市场的无风险利率为RQ+1之间的比例，即外部融资溢价成正比。假定其他条件不变，随着外部融资溢价上升，生产商的违约概率将下降。受此影响，一方面银行对于贷款趋于放松，另一方面生产商则在平均资本汇报相对增长的情况下更倾向于增加借贷并扩大企业规模。当然生产商的借款并非没有限度，在企业借贷规模不断上升并大幅超过净资产增长速度时，生产商的违约成本也将增加，在约束条件下最终还是转移给生产商自身。总体而言，生产商所筹集资本总额受到外部融资溢价以及企业净资产的综合影响，并非单纯某一因素可以完全决定。