银行局部均衡的约束条件及优化方案

考虑在不存在系统风险，且个体风险φM未知的情形下，假定生产商M所面临的市场平均资本回报率为，所需要筹集的资本总额为，贷款数额为，未违约条件下的贷款利率为，临界风险因子为φM。这里的临界风险因子φM是指生产商所可以承担风险的极限值，具体可表示为：

该式表明当生产商M面临的个体风险φM≥φM时，厂商除了归还贷款利息给银行后还有自己结余。但当φM＜φM时，则生产商由于资本回报不佳将无法归还原先规定的利息，存在违约行为。此时对于银行而言则不仅无法收回合约中规定的利息额，还由于审计成本的存在，仅可得到。将上述关系整理可得银行的实际贷款收益：

对于受生产商违约而造成的贷款利息减少，银行通常情况下固然会选择接受，但同样具有最低限度。假定市场本身的无风险利率为RQ+1，银行遵循期望收益等于机会成本原则(净利润为零的设定)，有以下均衡等式，其中F(φM)指生产商的违约概率：

将其化简：

将式5.1、式5.4代入以上等式，可得：

式5.8消去了未违约条件下的贷款利率为，从而将银行的均衡条件化简为临界风险因子φM的等式。观察等式左边，即银行的期望贷款收益是φM的函数。正如左式的构成，φM上升会给银行的期望贷款收益带来两方面影响：一方面增加了未违约条件下银行的贷款利息收入[1-F(φM)]φM·。另一方面，φM的增加意味着违约概率的上升，进而会减少整体的贷款利息额。

对于该问题的处理需对式5.8的左式进一步转化：

该式表明在机会成本约束条件下φM值的变动将决定生产商的融资总额在银行与生产商之间的各自分配比重。将左边中括号内式子继续转化，设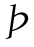(φM)为银行获得期望贷款收益所占总收益比重，可得：

对上式求导：

由于F(φM)∈[0，1]

所以

继续求导：

由于f(φM)∈[0，∞]

所以

基于式5.12及式5.14，可知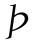(φM)的一阶导数为正，二阶导数为负，结合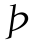(φM)本身特性可知其为增函数，且为凸函数。联系本研究，经济学含义为随着临界风险因子φM的增加，银行可获得的期望贷款总收益比重不断上升。(www.xing528.com)

但银行的可获得的期望贷款收益除了总收益外，还需扣除审计成本τφM·。设τ(φM)为银行的审计成本所占比重，可得：

且τ′(φM)=τφMf(φM)＞0，故τ(φM)为同样为增函数。

由式5.10及式5.15，可得：

银行可获得的期望贷款收益比重为(φM)-τ(φM)

重点分析(φM)-τ(φM)的函数特征：

由上文推导可知，(φM)-τ(φM)＞0，φM∈(0，∞)

进一步其求极限：

结合式5.2及式5.3的设定，ω(φ)=dF(φ)/1-F(φ)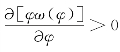，，对银行可获得的期望贷款收益比重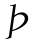(φM)-τ(φM)求一阶导数，得到其边际函数并化简为：

讨论该式：

由此可判断必存在一个φM*点，使

继续对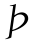(φM)-τ(φM)求二阶导数并化简：

综合式5.21及式5.22，可知银行可获得的期望贷款收益比重先增后减，且在φM为φM*处取得最大值。这一推导也保证了不存在信贷供给的情形。为方便起见，本研究假定φM始终低于φM*，换而言之，银行的期望贷款收益始终随φM而增加。

同样可以证明，在存在系统风险的情况下，上述结论依然是成立的。