小学数学应用题中的数学模型发展及建模教学

对于一个复杂的实际问题，要能从中发现其本质，建立其数量关系，转化成数学问题，没有扎实的数学基础知识、基本技能和数学思想、方法是不可能的。因此，进行小学数学应用题建模教学，首先要抓好数学应用题中的基本分类模型，抓好常见的数量关系，在此基础上，学会建立稍复杂的算术模型，再逐步学会建立代数模型、函数模型，才能切实提高学生的建模能力。

（一）小学数学应用题中的分类模型

过去，数学应用题教学中一种异化的做法是，按照问题情景，把应用题类型固化，专对一类情景归纳公式，而且凭强记、快做争取考试成绩，把路走歪了。自课程改革以来，对应用题不再做一些基本的分类和概括，实际上是作茧自缚、矫枉过正的表现。在小学数学应用题的教学中，对各种类型的数量关系的建模尤为重要。在日常生活中，教师需要引导学生用数学的眼光对数学存在的问题进行分析。在面对实际问题时，需要在脑海中搜索解决该问题的必要模型。如果仅仅凭借生活经验，舍弃各种类型的数量关系的建模，不能达到教学的初衷和要求。无论如何，无论中外，以下7种类型是必须正面提出、让学生认真学习的：行程问题，路程=速度×时间；工程问题，工作量=工作效率×工作时间；价格问题，总价格=单价×数量；利息问题，利息=本金×利率；利润问题，利润=成本×利润率；折扣问题，金额=价格×折扣率；百分数问题，数量=重量×百分比。我们的小学应用题，必须讲解这些类型。这些是典型的将生活问题抽象，建立出来的数学模型。这些概念是生活需要的常识，又是语文、社会等其他学科不会详细涉及的，将这些教学任务落在数学课上，责无旁贷。较复杂问题的模型往往由这些基本模型组合而成，所以让学生切实掌握这些不同类型的基本模型，是学生解决复杂问题的基础。关键是我们在让学生在建立模型的过程中，对它们进行基本的分类，需要对问题类型的内在结构有深入的了解，而不被表面言辞所左右。

例如，著名特级教师许卫兵的行程问题基本数量关系的教学案例：

师（出示交通标志）：这个交通标志表示什么意思？

生1：限速80千米。

师：限谁的速？

生2：汽车的速度。

（教师板书）

师：你知道什么是汽车的速度吗？

生1：按照汽车一小时行驶多少千米来算。

师：怎么知道汽车的速度？

生3：方向盘前面有表。

师：仪表盘上一个地方讲单位的名称。km/h，km是kilometer的简写，是千米的意思，h是hour的简写，是小时的意思，千米/小时，记作千米每小时，意思是每小时行驶多少千米。

师：老师3个小时行驶了240千米。我超速了吗？

生4：老师的速度是240÷3=80（千米），不超速。

生5：有可能你第一个小时超过了80千米，第二个小时不足80千米。

师：也就是说，80千米是我的平均速度。

师：红红2个小时行驶16千米，她的平均速度是多少呢？

生6：16÷2=8（千米/小时）。

师：直升机6分钟飞行48千米，平均速度是多少？

生7：48÷6=8（千米/分）。

师：宇宙飞船5秒飞行40千米，平均速度是多少？

生1：40÷5=8（千米/秒）。

师：看看这三道题，你有什么话要说？

生2：都是用路程÷时间=速度。

师：谁最快？

生3：宇宙飞船的速度最快。因为它是每秒8千米，直升机是每分钟8千米，红红则是每小时8千米。

师：看得见的东西在动，有快有慢。看不见的东西也在动，有哪些看不见的东西产生了速度？

生4：风。

教师出示电闪（光速）雷鸣（音速）。

师：先看到了什么？

生5：电闪，光速比音速要快。

师：对，光速是300000千米/秒，音速只有340米/秒。短跑比赛的时候，发令员在发令的同时打枪，为什么发令的同时还要打枪呢？

生6：因为音速慢，光速快，发令的同时打枪，计时员看到冒出的烟就开始计时，这样计时更准确。

师：老师以80千米/小时的速度行驶了4个小时，老师行驶了多少千米？

生7：80×4=320（千米）。

生8：速度×时间=路程。

师：老师以80千米/小时的速度行驶160千米，需要多少时间？

生1：160÷80=2（小时）。

生2：路程÷速度=时间。

师：从海安到北京要多长时间？需要知道什么？

生3：要知道速度。

生4：还要知道路程。

师：从海安到北京的路程大约是1200千米。自行车8千米/小时，飞机8千米/分钟，宇宙飞船8千米/秒，各需要多少时间？

生5：1200÷8=150（小时），骑自行车从海安去北京需要150小时，约6天。

生6：1200÷8=150（分），坐飞机从海安去北京需要150分，约2个半小时。(www.xing528.com)

生7：1200÷8=150（秒），坐飞船从海安去北京需要150秒，约2分半钟。

师：小红、小刚、小宇三人从家去学校，小红每分钟走60米，8分钟到校；小刚10分钟到校，每分钟走48米；小宇每分钟走60米，5分钟到校。三个人家到学校的路程各是多少米？

生8：小红家到学校是60×8=480（米）。

生1：小刚家到学校是48×10=480（米）。

生2：小宇家到学校是60×5=300（米）。

师：为什么速度÷时间=路程？（出示图）一个盘子3个苹果，4个盘子，可以怎样列式？

生3：3×4=12，12÷3=4，12÷4=3。

师：这里的每份数、份数、总数和前面的速度、时间、路程有什么关系吗？

生4：速度相当于每份数，时间相当于份数，路程相当于总数。

师：还有什么也有这种关系呢？

生5：单价×数量=总价。

生6：总价÷数量=单价。

生7：总价÷单价=数量。

生8：单价相当于每份数，数量相当于份数，总价相当于总数。

师：乘法其实就是一个框，好的东西就在里面装。

许卫兵老师的基本数量关系的这节课，很有特点。一是注重建模用模的问题情境的巧妙设计。从生活中的限速标志入手，让学生初步了解速度。三个求速度的问题依次是求红红、直升机、宇宙飞船的速度，三个速度正好依次是8千米/小时、8千米/分、8千米/秒，形象直观，便于学生进行速度快慢的比较，使学生对不同交通工具的速度快慢理解得更为深刻。求海安到北京的时间也依次是自行车、飞机、飞船，既激发了学生建模的兴趣，又使学生形象地理解了路程相同的情况下速度越快，用的时间越少，将函数思想悄然渗透其中。同时发令员发令的同时打枪这一生活问题情境也设计得很好，引导学生灵活运用模型去思考生活中的问题。二是注重在联系中让学生真正理解模型的本质。先沟通行程问题的三个关系，形成同一个模型。在此基础上，注重沟通速度、时间、路程和每份数、份数、总数、单价、数量、总价的联系，使学生真正理解所建立的行程问题的模型的本质，而不是将模型固化。讲死了，思维就变机械了。

因此，小学阶段应首先注重分类模型的教学，使学生掌握各种类型的基本数量关系，在面对实际问题时，能在脑海中搜索到解决该问题的基本的必要模型。在教学时，模型的题材呈现要独到、巧妙；模型的建立要抓住问题的本质，注重沟通同一类型模型的联系，加强不同类型模型的对比，使学生能真正理解各类型模型的本质；模型的应用要注重情境的变换，使学生在多种情境的解决中能够透过情境的表面抓住问题的本质，理解不同的问题情境可能本质是一样的，建立的是同一个模型。在学生掌握了多种基本模型后，也可通过同一问题情境引导学生从不同角度抽象归纳，建立不同的模型，培养学生灵活运用模型的能力。

（二）小学数学应用题中的算术模型

小学数学应用题的学习首先建立的是算术模型。有种设想是，完全抛弃算术解法解应用题，一开始就向小学生介绍方程解法。事实证明，这样学习的代数将成无源之水。正如双脚走路是基础，驾驶汽车不能取代走路。在学生掌握了常见的不同类型应用题的基本模型的基础上，遇到稍复杂一些的应用题，可以引导学生根据应用题的特征建立相应的算术模型。数学应用题是生活实际与数学糅合而成的产物，一半是数学问题，一半是生活实际，数学问题是应用题的内核。建立数学模型，就是要从应用题所描述的实际情况中，去伪存真，剥去穿在数学问题上的“外衣”，把数学信息抽出来，用它们来表示应用题的问题。因此，建立数学模型的第一步，就是要去掉应用题中与数学无关的内容，使数学信息与生活信息分离开。常见的模型形式有数学文字型模型、图式模型等。

1.数学文字型模型

这种模型是将数学应用题里无关紧要的生活情节去掉，抽象成只有数学文字表达的模型。例如：

甲、乙、丙三个组共有图书90本，如果乙组向甲组借3本后，又送给丙组5本，那么三个组所有图书的本数刚好相等。甲、乙、丙三个组原来各有图书多少本？

甲、乙、丙三组之间借来借去，条件真复杂。根据题意将数学信息抽取出来，用数学文字模型表达，问题就变得简单了。三人之间借来借去，没有借给别人，也没借别人的，所以三人相等，就是90÷3=30（本）。乙向甲借了3本，甲就少了3本，也就是甲的本数-3=30，乙向甲借了3本，就多了3本，又送给丙5本，就又少了5本，也就是乙的本数+3-5=30，乙送给丙5本，丙就多了5本，也就是丙的本数+5=30。这样通过把“送、借”这些生活化的字眼转化为数学上的“多了、少了”，再简化为“+、-”，就建立起这样的文字型模型：甲的本数-3=30，乙的本数+3-5=30，丙的本数+5=30。在此基础上，相应的算式也就出来了：甲30+3=33（本），乙30+5-3=32（本），丙30-5=25（本）。再将所得结果带到题目中检验：甲33-3=30（本），乙32+3-5=30（本），丙25+5=30（本）。说明模型建立正确，解答过程正确。这里文字型建模的关键在于语言的理解和转换，能否把通俗的语言翻译成数学语言，决定了建模是否成功和合理。

2.图式模型

图式模型是一种重要的数形结合的数学思想方法，它具有半抽象、半具体的特点，它既能舍弃应用题的具体情节，又能形象地揭示条件与条件、条件与问题之间的关系，明确显示出已知与未知的内在联系，激活学生的解题思路，就能化难为易、化繁为简、化隐为显。正如华罗庚先生所说的那样：“数无形时少直觉，形少数时难入微。数形结合百般好，隔离分家万事非。”

例如，在“替换策略”教学方面，包括倍数关系的等量替换和相差关系的等量替换。教学的重点是让学生充分理解替换策略的意义：把两种量替换成一种量，从而顺利地解决问题。难点是学生不易理解相差关系的等量代换，以及在解决问题时不知道该用什么方法来替换。李海峰老师在教学中引导学生建立图式模型，使复杂问题简单化、隐性条件外显化，既有效地突破了难点，又培养了学生的建模意识和建模能力。

李老师先创设情境，引导学生感知数学建模思想。出示应用题：

6个小杯和1个大杯一共是630毫升；一个大杯的容量相当于3个小杯的容量。小杯和大杯的容量各是多少升？

引导学生用画图感知（学生用○，即圆圈来表示图形），如图8-1、图8-2所示：

图8-1　学生画图1

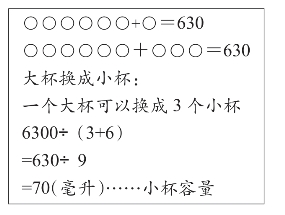
图8-2　学生画图2

在这个教学过程中，学生通过观察得出：解决这个问题需要把两种杯子换成一种杯子（即替换）。然后李老师引导学生画出示意图，即把直观图形抽象成几何图形，学生把直观图形抽象成几何图形的过程，其实是把生活中的原型上升为数学模式的过程。在这一过程中，学生初步感知了数学中的建模思想。

李老师接着提问：“是不是解决替换这类问题，都可以采用这种画图的模式来解决？”促使学生主动探究“该画怎样的图式模型才能解决这类问题？”从而使学生逐步抓住替换策略的本质。学生针对问题中的条件和问题之间的本质关系，做出合理的、简化的图式模型的假设。如图8-3、8-4所示。

图8-3　学生画图3

图8-4　学生画图4

学生通过假设的图式模型，梳理思路，提取原有的知识，形成较为完整的知识体系，能够清楚地抓住事物的本质关系，从而进一步解决问题。在这个过程中，学生由最初抽象的几何图形，到现在的数学表达式，恰恰体验了建立数学模型的过程，不仅培养了学生的建模意识，更为学生探究另一种数学模型增添了不少兴趣。

学生在以上问题的解决过程中，运用建立图式模型的方法，逐步理解并掌握了倍数关系的等量替换。接下来，李老师把题目中的条件换了一下：一个大杯的容量比小杯多140毫升。引导学生思考能不能用刚才建立的数学模型来解决。通过交流，学生明白了解决这个问题同样要把两种量替换成一种量，只不过在替换过程中，总量发生了变化。基于以上分析，引导学生建立这样的数学模型，如图8-5、8-6所示。

图8-5　学生画图5

图8-6　学生画图6

在建立图8-5、8-6的过程中，学生充分体验了形成数学模型的过程。学生根据建立的数学模型，对相差关系的等量替换的理解就较为容易。再让学生深入比较图8-3、8-4和图8-5、8-6两种图式模型的联系与区别，从而更为理解它们的本质。不仅让学生很好地掌握了重点，更突破了教学中的难点，解决这类替换问题也就水到渠成了。