【摘要】：整理数据，将问题数学化，如图7-1所示。图7-2如图7-2所示，问题可转化为：动点P在直线EF上运动，求长方形PHCG的最大值。在线段EF上取一点P，则公园面积取决于P点的位置。直线EF的方程是。
例：为了保护环境，实现城市绿化，房地产公司决定在拆迁地长方形ABCD处规划一块长方形地面建造住宅小区公园，公园一边落在CD上，但不能超过文物保护区AEF的EF边。问：如何设计才能使公园占地面积最大。设AB=CD=200m，BC=AD=60m，AE=60m，AF=40m。
【模型准备】
整理数据，将问题数学化，如图7-1所示。
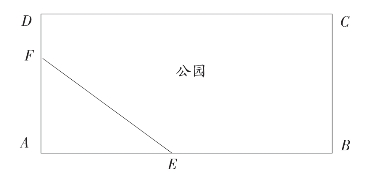
图7-1
【模型假设】
以CD为一边建造公园小区，又不能越过EF，因此公园PHCG的一角只能落在EF上，为此，以A为原点，AB方向为x轴，AD方向为y轴建立直角坐标系，如图7-2所示。
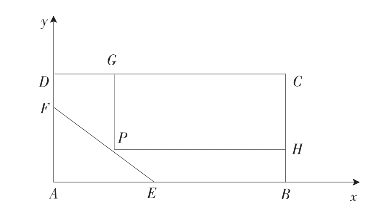
图7-2(www.xing528.com)
【建立模型】
如图7-2所示，问题可转化为：动点P在直线EF上运动，求长方形PHCG的最大值。
【模型求解】
在线段EF上取一点P，则公园面积取决于P点的位置。直线EF的方程是
。设P点的坐标为
，则长方形公园的面积为S=
。
可见，当x=10，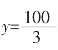
时，Smax=24067m2。
【模型应用】
问题：如何设计才能使公园占地面积为30000m2？
问题的解决：因为Smax=24067m2＜30000m2，所以公园占地面积不可能为30000m2。
评析：问题的解决过程体现了数学建模的思想，对模型应用的设计可加深学生对数学建模思想的理解。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
