(一)初中函数建模的概念
初中数学建模是用数学知识去解决实际生活中的问题,要求学生具备思维能力、逻辑能力与创新能力,将现实生活中的一些问题转化成数学知识来解答,经历提出问题、分析选择建模方法、确定模型的数学表达式、求解模型、回答问题的过程,培养学生用函数建模解决实际问题的意识,激发主动探索问题的欲望。初中数学建模运用适当的教学工具得到一个数学结构,数学结构是指数学符号、数学关系式、数学命题、数学图表等这些基于数学方法的数学问题。
通过实际生活中的实例,如学习正比例函数的建模,需要知道一次函数的解析式及其性质特点。理解是一个信息或要素组织的过程,如果没有达到一定的稳定程度,理解就很难进行。其作用包括推动迁移、促进记忆、影响信念。运用数学模型进行数学建模,然后把数学问题应用到实际生活中,对问题进行适当的修改,最后得到最理想的结果。学生能够清楚地明白,数学建模实际是一个桥梁,它将实际问题和数学问题连接起来,解决实际问题。数学建模教育,可以培养学生的观察力、想象力、自学力、洞察力,能够培养学生全面分析问题的能力,抓住问题的实质,为将来从事创造性学习和工作打下坚实的基础。
一般来说,初中函数建模是为了特定的目的,根据现实世界的特定对象进行识别简化、假设、设想,然后运用合适的数学工具建立模型,模型求解,得出结论。初中函数建模解决的是实际的问题,它要求我们把实际问题抽象成函数模型然后加以解决。从数学的角度出发,函数建模实际是对问题做一个数学模拟,将没用的信息排除,保留问题里的数学关系,用数学语言、符号和图形等形式来刻画、描述、反映具体事物之间关系的数学结构。通过某个问题,构造相应的函数模型,通过具体函数模型的研究来解决实际问题。
(二)初中函数建模的步骤
初中函数主要题型包括函数模型解析式确定问题,函数平移、对折、旋转问题,单调性和最值问题,图像与面积问题,数形结合问题,交点问题,选择最优方案问题,探究性问题,综合性问题,基于这些问题,在初中数学函数建模教学中需要掌握一次函数、反比例函数、二次函数的性质特点的前提下,在中学数学教学中,介绍如何运用数学函数模型和如何进行数学函数建模是学习、探讨以及进一步研究函数建模非常重要的途径。(https://www.xing528.com)
无论我们进行什么工作,总是想得到最好的结果。在实际生活中,初中以某种产品的销售为背景,以公司的工作业绩为背景,以公司装修所需材料为背景等这些都有一个共同的模式:有一个可以控制的变量,通过一些实际的限制,使某个其他变量达到最优化的结果。一般的一次函数建模有以下几种:两种方案的比较问题模型,优选方案问题模型,调配方案问题模型如用一次函数来解决坐标系中围成的面积问题,对称、对折、旋转问题。二次函数建模有以下几种:求图形面积的最值问题模型;最值利润问题模型;抛物线形问题模型,如解决运动员的跳跃轨迹、球类运动的轨迹、喷出的水的轨迹等。反比例函数建模有以下几种:解决工程问题模型、解决医药问题模型等。
(三)函数模型的基本图形
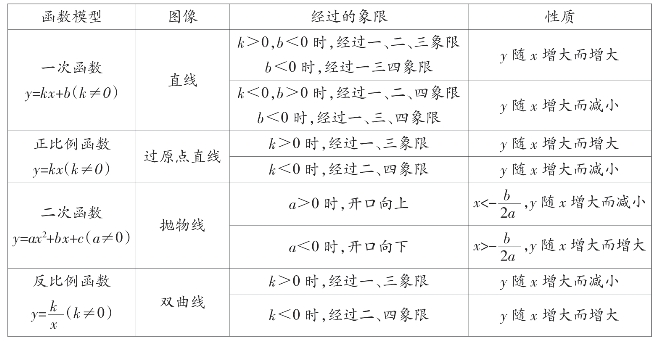
分别从一次函数、二次函数、反比例函数最优化模型来讨论。在选择具体模型时,我们应具备一定的函数模型,如表6-1所示。
表6-1 初中函数模型特点及性质
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




