小学方程教学内容分析及优化探讨

（一）小学方程的地位分析

小学方程内容在小学阶段有着很重要的地位，是小学阶段很特殊的教学内容。小学阶段，尤其是低年级和中年级，以算术知识的学习为主，数量关系也用数字符号来表示。而方程是使用字母符号表示数量关系，这与算术有着质的不同。方程是小学阶段代数部分的初步知识，在今后中学数学学习中，学生会接触到越来越多的代数知识，所以方程的知识有着重要的意义，它是学生的思维方式从算术思维向代数思维转化的关键转折点。对于小学生来说，实现从数字表示数量关系到用字母表示的转变，相对来说比较困难。所以，方程知识也是小学数学教学的一个难点，学生在初学时会有一些不适应，需要教师重视对这一内容的教学并加以合理的引导。总的来说，方程是小学阶段数学教学的重点和难点，占据着很重要的地位。

（二）小学方程的内容结构

小学阶段方程学习的内容主要包括：用字母表示数、方程的意义、不等式的基本性质、解方程和列方程解决实际问题。其中，用字母表示数，是学生最先学习的知识，其被安排在四年级下册，但其思想在低年级就已经渗透过了。学生最初接触的用字母表示数是用字母表示计算公式，由于长期这一思想的渗透，学生对于用字母表示数的知识，并不难接受，这为学习方程知识奠定了良好的基础。由于方程也是一种等式，研究方程的意义要从等式的知识过渡，等式的学习是方程的基础，解方程的直接依据是等式的性质，在学习解方程前，学生应当已经掌握了等式的性质。在掌握了方程的意义和解方程以后，学生会用方程解决实际问题。方程知识的内容结构如下图5-1所示。

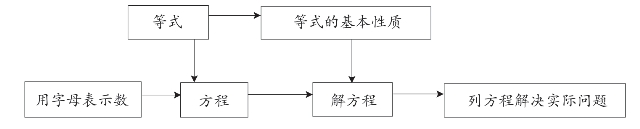
图5-1　小学方程内容结构示意图(www.xing528.com)

（三）在方程教学中渗透模型思想的优势

基于上述对方程数学内容的分析，可以知道方程知识在小学数学知识体系中占据着重要的位置，实现了学生从算术领域向代数领域的过渡，并为学生高等代数的学习奠定了良好的基础。方程模型是数学模型中一种极其重要且常见的模型，对学生模型思想的建立和数学应用能力的培养，有着重要的意义。在几大数学模型当中，在小学阶段出现的仅有方程模型，可见方程模型的重要地位。此外，最为重要的是方程知识的教学对于培养学生数学应用能力的巨大作用。对于亟须培养学生的数学应用能力，可以通过方程知识的适当教学，得到很大程度的提升。

学生在面临简单的实际问题时，可以先通过对问题的分析，使之成为简单的数学模型，转化为一元一次方程，通过解方程，也就是求解模型，得到方程的解，再回归到实际问题中去检验，也就是模型检验，最后服务于实际生活。这是一套完整的数学建模的过程，所以在学生学习方程知识时，每解决一个问题，便是一次数学建模的过程，便是模型思想渗透的过程。如果教师能够积极引导学生，让方程的学习不再是机械的做题训练，而是有趣的数学建模，那学生的数学应用能力会得到很大程度的提升。笔者正是基于方程知识和方程模型的重要地位以及方程对培养学生的数学应用能力的贡献，认为在小学数学教学中进行渗透模型思想的教学实践，方程是最为合适的选择。

（四）基于数学建模思想的小学方程教学的重要性

数的认识、数的运算、方程等是小学阶段“数与代数”的主要内容。纵观九年制义务教育，方程处于承前启后的地位，方程的学习是在学生学习了算术知识的基础上进行的，小学生主要是以算术学习为主。到了高年级，学生会接触到越来越多的代数知识，它为初中不等式以及函数的学习奠定了坚实的基础，因此，方程的学习具有重要意义。方程是代数思维的典型代表，小学阶段方程学习的目的就是在孩子心中埋下一颗代数的种子，使他们的思维发散开来，具有多元化，既包括算术思维又包括代数思维，为初中的学习做好铺垫。因此，方程的教学内容在小学阶段具有至关重要的作用。

在众多数学模型中，方程模型在小学阶段是比较典型的，而且是最为常见的一种数学模型，因此方程模型具有十分重要的作用。学生应用能力的提升是数学学习的价值体现，基于模型思想的教学渗透对此帮助巨大。