高中数学建模教学设计方案

因为高中数学中数学建模的类型比较全面，以下将以高中数学建模教学设计为例，对这几种主要的数学模型进行介绍。

（一）集合模型

集合模型主要是在数学建模活动中，建立数学模型集合是数学的基础，在高中数学课程中，集合是刻画一类事物的语言和工具。经过集合的学习能够用其语言简洁、准确地表述数学的研究对象，学会用数学的语言表达和交流数学问题。

【例1】某高中为了积极响应国家培养学生全面发展的号召，以及加强学生身体锻炼的目的。学校决定组建乒乓球队、篮球队、足球队，每位同学根据自己的兴趣爱好，可以多报，也可以不报。据统计，高中部一共有200人报名参加，其中参加乒乓球、篮球、足球队人数分别为：150、136、122。其中，同时报名参加乒乓球和篮球队34人，同时报名参加乒乓球和足球队24人，三项都报名参加有12人，求同时报名参加足球和篮球队的人数，以及只报名参加乒乓球队的人数。

模型准备：

1.把题目中的语言文字转化为相应的数学符号（见表3-1）

表3-1　语言文字对应的数学符号

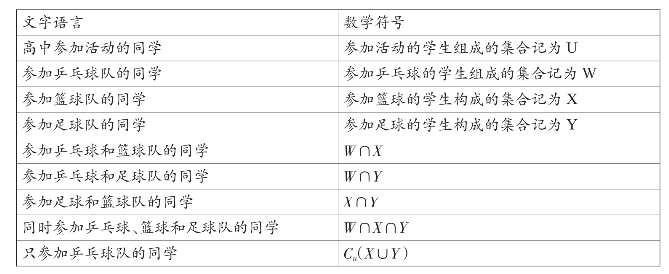
2.其中的数量关系用数学符号表示，用n（A）表示集合A中元素的个数：

n（U）=200n（W）=150n（X）=136n（Y）=122

模型假设：理清各个集合之间的关系。

模型建立：根据题意可以建立如下模型：

n（U）=n（W）+n（X）+n（Y）-n（W∩X）-n（W∩Y）-n（X∩Y）+n（W∩X∩Y）

即n（X∩Y），n[Cu（X∪Y）]

模型求解：

因为n（U）=200，n（W）=150，n（X）=136，n（Y）=122，n（W∩X）=34，n（W∩Y）=24，n（W∩X∩Y）=12

所以200=150+136+122-34-24-n（X∩Y）+12

所以n（X∩Y）

因为n（X∩Y）=n（X）+n（Y）-n（X∩Y）

所以n（X∩Y）=136+122-162

所以n（X∩Y）=96

所以n[Cu（X∩Y）]=104

【模型分析】

上面建立的模型应用了集合元素的数量关系。通过将现实生活中的数量关系转化到集合元素的数量关系，既简单又准确。在实际生活中，很多雷同问题也可以用这种方法进行计算。

【模型检验】(https://www.xing528.com)

在班上模拟成立3个兴趣小组，组织学生现场报名，每个同学可报多个，进行统计。先给出每个小组的人数，报2个小组的情况，再用上面的模型算出同时参加3个兴趣小组的人数，与实际统计人数做比较，进行检验。

【模型应用】

参加一些兴趣班、活动等，一人可报多个项目时，可以根据上面的模型找到到底多少人报了哪些项目，为活动安排做准备。

集合是一类重要的数学语言，是数学的根基，也是数学的基础知识。一般来讲，集合是学生进入高中学习的第一个知识点，很多学生觉得集合太过于抽象，学习起来非常困难，并且觉得集合就是纯数学知识，与生活实际没有什么联系，不懂也不会主动询问教师，只会对集合的学习越来越没有信心。集合是数学的基础，如果一开始就失去信心是没办法进行后续学习的，教师必须想办法调动学生学习的兴趣，在生活中找到应用集合知识的问题，使学生切实体会到集合不但在数学中是重要的内容，在生活中也是有用的。在上面设计的题目中，在学校选修课程人数确定时，集合的相关知识就体现出实用价值。另外，学生还可以根据此题进行引申，解决更多的实际问题。

（二）函数模型

函数是现代数学中最基本的概念，是描述客观世界变量关系和规律的最为基本的数学模型和工具，有着广泛的实际应用。函数作为高中数学学习的主线，贯穿于高中学习的每一部分知识。有关函数的数学模型，根据函数的类型不同可以分为一次函数模型、二次函数模型、指数函数模型、对数函数模型、幂函数模型、三角函数模型等。

（三）向量模型

向量的引入为数学的学习、应用增加了一个工具。最初，向量主要应用于物理学，很多物理量，如力、速度、电场强度、磁感应强度等都可以用向量表示。从与物理的联系上可以看出，向量在实际生活中的应用范围是比较广泛的。

【例2】长江两岸之间没有大桥的地方，常常通过轮渡进行运输，一艘船从长江南岸A点出发，以5km/h的速度向垂直于对岸的方向行驶，同时江水的速度问向东2km/h。请问：这艘船需要多久才能到达对岸？

（四）统计与概率模型

统计和概率在实际生活中具有广泛的应用性，是对某件事情发生的可能性进行说明，个人消费、投资理财、天气预测等都需要应用统计和概率的知识，社会、生活的方方面面都离不开统计与概率。我们正处于一个大数据时代，掌握对数据的收集和处理是十分有必要的。在学生学习这部分知识时，适当地加入一些现实实际问题，让学生真切感受到其实用性。

【例3】甲、乙是两艘大型货运船只，这两只船驶向一个不能同时停靠两艘大型船的码头，这两只船在一昼夜内到达这个码头的时间是等可能性的。如果甲船停靠的时间为1小时，乙船停靠的时间为2小时，它们中任意一船都不需要等待的可能性多大？

（五）数列模型

数列是高中数学学习的重要知识点之一。数列是一类特殊的函数，用图像的表示方法来表示数列，得到一族离散的点，这是由于数列这个函数的定义域是正整数集，是非连续的，所以得到的图像是离散的点。通过对数列的学习感受数列与线性函数的联系与差异，体会知识之间的相互联系与区别，体会数学的整体性。

【例4】某市为了改善居民的居住条件，决定着手扩大城市绿化面积。据此提出了实施总目标：从今年起用10年的时间，在全市范围内整治城市绿化。据测算，2017年该市用于城市绿化的工程经费大概要50万元，为了创造更好的生活环境，计划之后每年投入的资金都比上一年多5万元。那么从今年起的10年内，该市在绿化工程中的总投入是多少？

（六）不等式模型

不等式能反映事物之间量的大小关系，能够直观地刻画实际生活中的不等关系，是研究数量关系的重要工具和手段。

【例5】社会稳定和谐是经济发展的大前提，一般情况下，在社会出现动荡时，经济都会受到很大影响。香港“占中”行为就对香港造成重大经济损失，为了恢复经济，各大厂家、工厂纷纷拿出自己的解决策略。某厂家为了挽回经济损失，决定趁春节进行一场促销活动。经预算当某产品促销费用为x万元时，销售量t（万件）满足关系式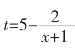：。假定生产量等于销售量，当生产该产品t万件时还需要投入成本（10+2t）万元（不含促销费用），产品的销售价格定为（4+20/t）万元/万件。促销费用投入多少时，厂家的利润最大？

（七）导数模型

导函数是为了进一步研究函数的性质，根据导函数可以求得函数的增减性，这是求函数的最值问题常用的方法之一。

【例6】山区外围有两条互相垂直的直线型公路，公路是山区发展的生命线，计划修一条连接两条公路和山区边界的直线型公路。记两条互相垂直的公路及山区边界曲线分别为l1，l2，C，计划修的公路为l，其中M，N为C的两个端点，测得点M到的距离分别为5千米和40千米，点N到l1，l2的距离分别为20千米和2.5千米。在修路之前一定要做好规划，山区地势复杂，往往会导致修路花费比较高，所以路线规划显得尤为重要。以所在的直线为x、y轴，建立直角坐标系。假设曲线符合函数y=a/x2+b（其中a，b为常数）模型。如何修建这条公路使得所花费用最少？

（八）综合模型及复杂模型列举

在学生对数学建模有一定的了解，并且能够自主解决一些简单模型的数学建模问题的基础上，综合模型和复杂模型是进一步深入了解、认识数学建模所必须要学习的。综合模型和复杂模型的数学建模问题与简单模型的数学建模问题相比较，从知识上看变得综合了，涉及的数学知识是多方面的；难度也增加了很多，有的学生初次接触可能不知道突破口在哪里；这些题型更加接近学生的实际生活。

【例7】目前电的使用涉及我们生活的方方面面，看到这么一句话形容电的重要性，“如果一天没有电，就感觉自己生活在原始社会”。这句话虽说有点夸张，但还是把电的重要性体现出来了。发电是需要成本的，那我们用电就需要交电费。为了避免过度浪费，国家对电费实行梯度定价，那请同学们自行了解什么是梯度电价，整理出用电量与所交电费之间的关系，并估计自己家每月的电费。