数学建模的思想和概念分析

（一）数学模型

数学模型首先是一种形式模型或符号模型。关于数学模型的定义，各种文献、书籍中都有所呈现，并且趋于一致。例如，张奠宙和过伯祥两位教授认为：“数学模型就是将一种事物或者在其运动的过程中，运用数学的方式、思维以及逻辑关系从数量上描述出来，使人们对于数量关系的认识更为深刻、确切。”除此之外，徐利治教授认为：“数学模型相对于一些事物的特征或数量关系的一种参照，采用数学化的形式，描述出来的一种数学结构。”对这种结构的阐述，美国数学及其应用联合会编写的《数学的理论与实践》一书中认为：“数学模型是观察变量之间关系的一种数学结构。”这里的数学结构有两方面的要求，首先这种结构是纯关系结构，是经过数学抽象地除去了一切与关系无本质联系属性后的系统；其次，这种结构是通过数学概念和数学符号来描述的。除了对数学模型是一种数学结构的解读，王宪昌将数学模型定义为“针对现实中某事物系统的特征或数量关系，采用数学概念、符号或数学语言表述出来的关于事物系统与研究目的有关的本质特征的关系结构”。

综上可知，数学模型指的是通过数学的方式来呈现现实中的模型，是对实际的对象的一种刻画。数学模型分为广义和狭义两个方面，从广义上讲，一切数学都是数学模型，包括数学中的各种概念、公式、理论体系及对数学理解中的算法体系，都是在各自相应的原型实体中抽象出来，是实体特征及数量关系的纯数学结构。从狭义上讲，数学模型是将具体事物抽象出来构成一种特定的数学关系结构，只有反映那些特定问题或事物系统的数学结构才叫数学模型。

（二）数学建模

用数学解决实际问题时，就要用数学的语言、方法去近似地刻画该实际问题，这种刻画的数学表述就是一个数学模型，其全过程就是数学建模。

实际上，数学建模是一个复杂的过程，通常需要经过多次循环，即需要从实际情景中找出需要研究的现实问题，经过假设、简化和抽象抓住问题的主要方面，建立初步的数学模型，对模型进行求解，通过检验找出模型存在的不足，然后再对实际问题进行假设、简化、抽象，改进数学模型，再次求解，并接受实践的再检验，如此循环多次，直到得到较为理想的结果。

虽然人们对数学建模有多种表述，但是，对于上面所阐述的数学建模过程都持认可态度。数学建模的过程可用图1-1表示出来。

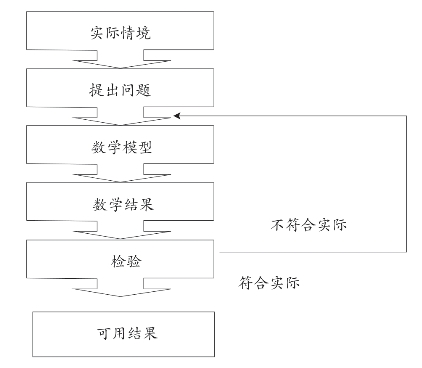
图1-1　数学建模过程

从图1-1可以看出，数学建模体现的是一种微型科研过程。通过数学建模，学生既学到了数学知识，又提高了数学应用意识和应用数学解决实际问题的能力，同时也提高了获取和处理信息的能力、主动探究和分析解决问题的能力、与人合作和终生学习的能力。因此，数学建模被逐渐引入教育、教学当中是社会发展的必然趋势。

（三）数学思想

数学的本质是研究空间形式和数量关系的科学。数学思想是指数学本质反映到人们的意识之中，经过思维活动而产生的结果。高中数学常用思想包括函数与方程思想、数学结合思想、分类与整合思想和转化思想。同时，数学思想还包含方程思想、整体思想、类比思想、建模思想、极限思想等。通过数学思想的培养，数学的能力才会有一个大幅度的提高。掌握数学思想，就是掌握数学的精髓。

（四）数学建模思想

数学建模思想是数学学习的基本思想之一，也是现代教学中的重要思想，贯穿着整个教学过程，新课程标准指出，建立和求解模型的过程包括四个方面：第一，理解现实生活或者具体情境中想要解决的问题，从中抽象出数学问题；第二，运用适当的数学符号建立方程、不等式、函数等用来表达数量关系以及变化规律；第三，求出所建表达式的结果并且检验结果是否正确；第四，讨论结果具有的现实意义。理解甚至掌握这些内容不仅有助于学生形成模型思想，而且可以提高学生学习数学的兴趣和应用意识，要知道兴趣才是一个人最好的教师。(www.xing528.com)

数学建模的基本思想是以某一理论为依据，通常是基于对数学理论的把握，再结合对问题的理解和看法。而理解和看法并不是可操作性的东西，很多人认为它很简单，就是一种感觉，其实不然，它包含了一个人知识的积累和经验的沉淀。数学建模比赛就是思维的碰撞和灵感的体现。

（五）数学建模能力

1.数学建模能力

吴长江认为，数学建模能力是指把问题数学化，建立适当的模型，求出结果带回问题中检验，最终对问题做出合理的解释。许二龙指出，数学建模能力是学生经历数学建模过程中所收获的经验、技能等的总和。数学建模能力可以体现在理解问题和分析问题的能力、抽象概括能力、思维能力、合理推理能力、演绎推理能力、运算能力、问题解决能力。

2.数学建模能力相关分析

数学建模能力泛指设计、创造或建立数学模型的能力，具体地说，是数学建模活动体现出的全面的数学能力。

一是“翻译”能力，即能将日常语言描述的实际问题用数学语言表达成数学问题，建立数学模型，并把数学问题的解用大众能理解的非数学语言表达出来的能力。

二是数据处理能力，即学生对所搜集数据确定有效性、区分主次，并找出关键性数据进行分类、整理、抽象、归纳的能力。

三是运用数学工具的能力，即用数学工具对所建立的数学模型做数学分析、推理及计算的能力。

四是创造能力，即学生创造性、丰富的想象能力以及洞察力的发挥。

五是其他能力，包括交流、合作、表达及写作能力，建模活动要求在小组讨论和合作中学生倾听别人的意见，在争论中获得启示并分享建模成果。

（六）数学建模教学

数学建模教学是指在数学教学中，教师结合数学课本内容，将未经简化抽象的现实生活问题带到教学活动中，引导学生在数学课堂、数学活动、课后思考以及生活实际中更好地运用观察、理解、抽象、概括、比较、分析、综合等基本数学思维方法，最大限度地调动已获得的数学知识，以数学的眼光研究实际生活中的问题，建立相应的数学模型来解决实际问题的教学过程。在这一过程中，学生首先遇到的问题是用数学的眼光看问题，将现实问题抽象成数学问题。在这一转化、抽象的过程中，如何有效地将数学知识进行迁移起着至关重要的作用。其中，精选材料；注意教学材料与程序的编排；改进教材呈现方式；促进教学方法多样化提高知识的概括化水平；教授学习策略，培养学生的迁移意识等都可以有效地促进学生灵活运用知识，将数学知识迁移到实际问题中的能力。因此，研究分析建模教学状况以及建模数学教学的现状的原因，找到更合适的建模教学方法，提高学生问题解决能力等，具有重要的意义。