探索有趣的剪拼正方形

材料来源：

上海教育出版社《九年义务教育课本数学七年级第二学期》。

知识平台：

实数的概念、用数轴上的点表示实数。

拓展意义：

无理数的发现，是人类对数认识的一次飞跃，也是生产和生活实际的需要。在伴随无理数的产生过程中，有很多相关史料和一些人文材料，比如本课就是以古希腊的毕达哥拉斯学派发现有理数的数学小故事为背景，引导学生动手操作证明无理数的存在性，并且在此基础上对数学知识进行拓宽，研究面积为2，3，5…的正方形边长等。所以本节课通过剪拼正方形的拼图游戏，学生动手动脑，把几何与代数结合起来，对培养思维能力，激发学习兴趣，拓展学生的数学人文修养，都有拓展的意义。

活动建议：

活动一带领学生听故事走进数学史。活动二较简单且课堂上易操作，建议在课堂内完成。活动三有一定的难度，建议引导部分学有余力的学生组成学习小组利用课余时间思考论证，在学生发现了活动三的剪拼方法2之后，教师可引导学生发现总结规律，将剪拼正方形问题推广到活动四和活动五。

活动方案：

活动一：聆听数学小故事

教师给学生讲数学故事：公元前500年，毕达哥拉斯学派的弟子希伯索斯（Hippasus）发现了一个惊人的事实，一个正方形的对角线与其一边的长度是不可公度的（若正方形的边长为1，则对角线的长不是一个有理数），这一不可公度性与毕氏学派的“万物皆为数”（指有理数）的哲理大相径庭。这一发现使该学派领导人惶恐，认为这将动摇他们在学术界的统治地位，于是极力封锁该真理的流传。希伯索斯被迫流亡他乡，不幸的是，在一条海船上还是遇到毕氏门徒，被毕氏门徒残忍地投入了水中。后来人们知道，这是一个伟大的发现，是人类理性智慧的胜利。

活动二：将两个大小一样的正方形，拼成一个正方形

教师提问：如何将两个大小一样的正方形，剪拼成一个正方形？

学生论证：将两个大小一样的正方形沿对角线剪开，以对角线为边长构造一个正方形。（图1）此时设原有两个正方形边长为1，易知大正方形的面积为2，则边长为。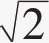

图1

活动三：将三个大小一样的正方形也拼成一个正方形

教师提问：如何将三个大小一样的正方形，剪拼成一个正方形？

学生论证：（剪拼方法1）可先将三个正方形中的两个沿对角线剪开，然后拼成图2的中图，联结AB、BC、CD、DA，将画阴影的四个三角形剪下，补到黑块上去，就得到一个大正方形了。(www.xing528.com)

图2

为什么阴影三角形割补到黑块上去呢？这是因为DG∥AE，DG=AE，四边形AEDG是平行四边形，所以对角线AD、EG互相平分，即EF=FG，AF=FD，于是△AEF≌△DGF。

学生论证：（剪拼方法2）可先将三个正方形中的两个沿对角线剪开，一个两次沿对角线剪开，然后拼成图3的中图，同样联结图中各顶点，证明方法如剪拼方法1。

图3

活动四：将五个大小一样的正方形拼成一个正方形

教师提问：如何将五个大小一样的正方形，剪拼成一个正方形？

学生论证：由活动三的剪拼方法2，归纳出如下规律： 用尽可能多的小正形（如：3=2+1，5=4+1，6=4+2）拼成中间正方形，然后把剩余的小正方形分成4个形状和大小一样的直角三角形，并把这4个直角三角形按一定顺序摆放在4条直角边上，最后连接各个直角顶点，所形成的四边形一定是剪拼后的正方形。所以，5个大小一样的正方形也可拼成一个大正方形，如图4。

图4

活动五：将五个同样大小的正方形，剪拼成两个相等的大正方形

教师提问：如何将五个同样大小的正方形，剪拼成两个相等的大正方形？

学生论证：设每个小正方形的边长为a，则每个小正方形的面积为a2，五个小正方形的面积之和为5a2，因而拼成的每个大正方形的面积为，那么每个大正方的边长为

如图5，如果把三个小正方形并列在一起形成一个矩形ABCD，则由勾股定理可知，矩形对角线AC=，假设O为AC的中点，那么AO=OC=，正好等于拼成的两个大正方形的边长。因此如果过O点作直线EF⊥AC，则EF与AC对由三个小正方形组成的矩形ABCD分割。这时，由对称性，如图6，我们把另外两个小正方形放在矩形ABCD上下各一个，使得五个小正方形组成一个十字形，对角线AC与EF把整个十字形分成四个部分，其中任意两个部分可以拼成一个大正方形。

图5

图6

活动小结：

因为活动三有一定的难度，所以本课题并不适合所有活动都在课堂当场生成。笔者在执教时，活动三中的剪拼方法2是学优生在课后思考了一个月之后才给出的答案。学生这种遇到困难不放弃，敢于接受挑战的学习品质难能可贵。教师在学生的启发下，继续设计了活动四和活动五，让学生继续深入思考总结规律，并以“有趣的剪拼正方形”为题，撰文发表在《初中生世界 智慧数学》2015年2月期刊上。这是一个教学相长的典型案例。