1.对指标数据进行标准化处理
由于评价体系所选取的各个指标数据的量纲不同，在进行因子分析之前，必须对数据进行标准化处理。SPSS软件在此提供了一种简易方便的数据标准化方法——Z-score标准化方法，即每一变量值与其平均值之差除以该变量的标准差。无量纲化后的各变量的平均值为0，标准差为1，从而消除量纲和数量级的影响，然后再利用统计分析软件SPSS18.0对标准化后的数据进行因子分析。标准化处理公式如下。
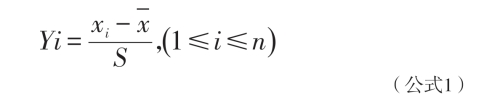
其中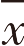
为所有样本数据的均值（见公式2），s为所有样本数据的标准差。
2.可靠性检验和KMO检验
在因子分析之前，需要对所选数据是否适合做因子分析进行检验，在此采用可靠性检验和KMO检验。
（1）可靠性检验
在SPSS18.0中利用可靠性分析对数据进行Cronbach’s Alpha检验，结果见表3。
表3 可靠性检验输出结果
Cronbach’s Alpha系数达到了0.8以上，说明所选数据是可靠的。
（2）KMO检验
此后又对所选数据进行KMO检验，结果如表4所示。
表4 KMO检验结果
如表4所示，KMO=0.795，＞0.5，巴特利特球体检验P值为0.000，小于0.01，说明数据具有相关性，能够用于因子分析中。(www.xing528.com)
3.确定主因子
运用SPSS18.0软件对上述原始数据进行处理，根据特征根大于1、累计方差贡献率不小于80%的原则，从中选出了4个主因子，其累计方差贡献率达到了100%，这说明所选的4个主因子能够解释原始24个指标变量100%的信息。由此证明文章所收集的数据准确率较高，能够较好地体现样本城市的核心竞争力水平。表5为各主因子的特征根和方差贡献率。
表5 主因子表
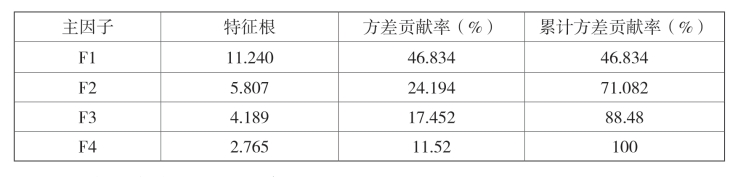
4.载荷矩阵说明及主因子命名
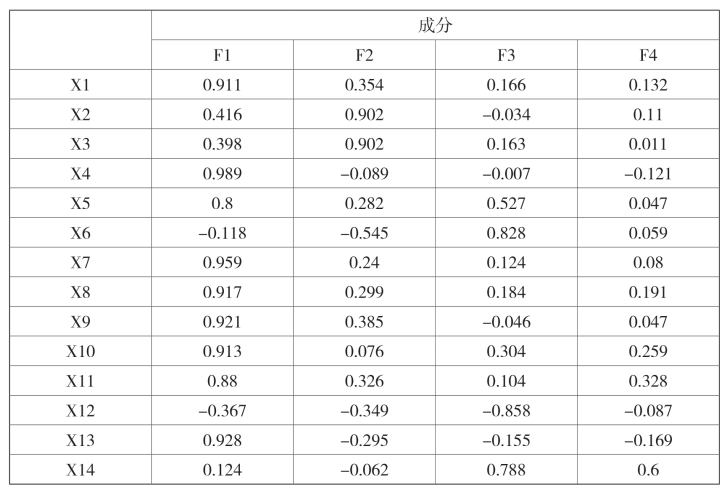
对数据进行处理后，便可以得到初始载荷矩阵，发现其结构不清晰，有些变量的因子归属不确定，不能较好地解释和说明原始变量。因而，课题组对载荷矩阵按照方差最大原则进行旋转，使载荷量出现两极分化的状态，从而达到简化结构的目的。表6即为旋转后的因子载荷矩阵，通过对各个指标的载荷因子分析，找出对主因子更有解释力度的关键指标。
表6 旋转后的因子载荷矩阵
续表
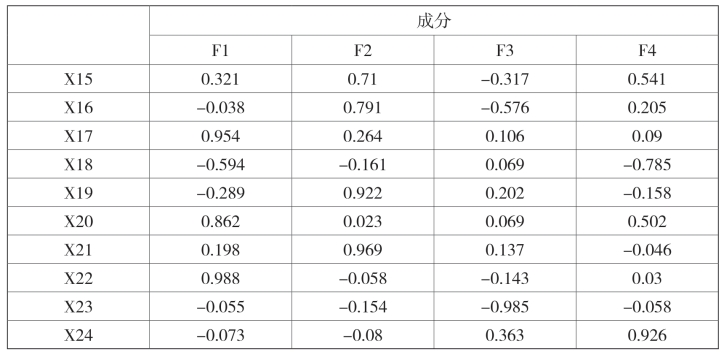
注：因子旋转方法为最大方差法。
在载荷矩阵中，载荷系数的绝对值越大，说明主因子对原变量的解释能力越强。由表4可知，第1主因子F1在X4、X22、X7、X17、X13、X8、X9中载荷系数比值较大，主要反映了城市综合经济实力水平，因此将其界定为经济实力因子。第2主因子F2在X21、X19、X2、X3、X16中载荷系数比值较大，突出体现了城市科教发展水平，因此将其界定为科技教育因子。第3主因子F3在X23、X12、X14、X6中载荷系数比值较大，主要展示的是城市基础设施建设状况，因此将其界定为基础设施因子。
第4主因子F4在X24、X18中载荷系数比值较大，侧重反馈了城市的对外开放程度，因此将其界定为对外开放因子。
5.因子得分及其排名
根据因子得分系数矩阵表中的得分系数，再用SPSS18.0软件做回归，得到各个主因子在各个城市的得分，即F1得分、F2得分、F3得分和F4得分。然后再将各个主因子的得分乘以各自的方差贡献率，相加求得各个城市的F综合得分。根据表3.6可以看出，根据F综合得分的排名，所选5个城市的核心竞争力依次为南宁、柳州、桂林、玉林、钦州。再按照分项因子进行排列的话，主因子F1（经济实力因子）得分中柳州位居第二；主因子F2（科技教育因子）的排序中，柳州位居第一；柳州排在主因子F3（基础设施因子）中的第三位；若按照主因子F4（对外开放因子）排位，柳州则排在第四名。由此可以判断，柳州在5个所选城市中，综合经济发展实力和科技教育水平更具核心竞争力；而在基础实施及对外开放方面，则与位居第一的玉林、桂林等城市存在较大差异，制约城市核心竞争力提升的短板因素凸显。
表7 城市核心竞争力排名表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
