中部地区TFP增长的实际考察和估算

(一)TFP的估算方法

在经济增长核算理论中，全要素生产率最早由索洛(Solow，1957)提出，故也称为索洛余值。^[36]TFP指各要素(如资本和劳动等)投入之外的资源优化配置和技术进步等因素导致的产出增加，是剔除要素投入贡献后所得到的余值，等于产出增长率与全部投入要素增长率加权和之差。估算TFP的常见方法有两种：一种是增长核算方法，其理论模型简洁，来自新古典增长理论，是一种非参数的经验估计方法；另一种是经济计量学方法，一般将总产出或增加值作为因变量，将不同的投入变量作为自变量，通过参数估计的方法来进行估算。

1.增长核算方法

增长核算法的基本思路是以新古典增长理论为基础，将经济增长中要素投入贡献剔除掉，从而得到全要素生产率增长的估算值，其本质是一种指数方法。按照指数的不同构造方式，可分为代数指数法和几何指数法(也称索洛残差法)。

(1)代数指数法。

代数指数法最早由艾布拉姆威兹(Abramvitz，1956)提出，其基本思想是把全要素生产率表示为产出数量指数与所有投入要素加权指数的比率。^[37]

假设商品价格为Pt，数量为Qt，则总产出为PtQt。生产中资本投入为Kt，劳动投入为Lt，资本价格即利率为rt，工资率为wt，则总成本为rtKt＋wtLt。在完全竞争和规模收益不变假设下，有总产出等于总成本，即：

PtQt＝rtKt＋wtLt　(3-9)

但由于技术进步等因素的影响，(3-9)式往往不成立，可将上式改写为：

P0Qt＝TFPt[r0Kt＋w0Lt]　(3-10)

其中，r0、w0和P0为基年利率、工资和价格。参数TFPt为全要素生产率，反映技术进步等因素对产出的影响。所以：

TFPt＝P0Qt/[r0Kt＋w0Lt]　(3-11)

(3-11)式就是全要素生产率的代数指数公式。后来，经济学家们又提出各种全要素生产率代数指数，它们的形式虽不同，但基本思想是一样的。代数指数法很直观地体现出全要素生产率的内涵，但缺陷也十分明显，主要体现在它虽然没有明确设定生产函数，但暗含着资本和劳动力之间完全可替代，且边际生产率是恒定的，这显然缺乏合理性。所以，这种方法更多的是一种概念化方法，并不适于具体实证研究。

(2)索洛残差法。

索洛残差法最早由索洛(Solow，1957)提出，基本思路是估算出总量生产函数后，采用产出增长率扣除各投入要素增长率后的余值来测算全要素生产率增长，故也称生产函数法。在规模报酬不变和希克斯中性技术假设下，全要素生产率增长就等于技术进步率。

总量生产函数为：

Yt＝A(t)F(Xt)　(3-12)

其中，Yt为产出，Xt＝(x1t，…，xnt)为要素投入向量，xnt为第n种投入要素。假设A(t)为希克斯中性技术系数，意味着技术进步不影响投入要素之间的边际替代率。进一步，假设F(·)为一次齐次函数即关于所有投入要素都是规模收益不变的。(3-12)式两边同时对时间t求导，并同除以(3-12)式有：

其中，为各投入要素的产出份额。由(3-13)

式有：

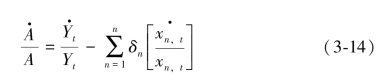
(3-14)式就是全要素生产率增长的索洛残差公式，本质上是一个几何指数。索洛残差法开创了经济增长源泉分析的先河，是新古典增长理论的一个重要贡献(Lucas，1988)。^[38]但它也存在着一些明显缺陷：索洛残差法建立在新古典假设即完全竞争、规模收益不变和希克斯中性技术基础上，这些约束条件很强，往往难以满足；具体估算中，由于资本价格难以准确确定，所以利用资本存量来代替资本服务，忽略了新旧资本设备生产效率的差异以及能力实现的影响。此外，索洛残差法用所谓的“残差”来度量全要素生产率，从而无法剔除测算误差的影响。上述这些因素都不可避免地导致全要素生产率的估算偏差。

2.经济计量方法

由于增长核算法存在着较多缺陷，后来人们提出很多经济计量方法，以期借助各种经济计量模型和计量工具准确地估算出全要素生产率。我们主要比较两种计量方法，即隐性变量法和潜在产出法。

(1)隐性变量法。

隐性变量法的基本思路是，将全要素生产率视为一个隐性变量即未观测变量，从而借助状态空间模型利用极大似然估计给出全要素生产率的估算。

因为产出、劳动力和资本存量数据的趋势成分通常是单位根过程且三者之间不存在协整关系，所以，往往利用产出、劳动力和资本存量的一阶差分序列来建立回归方程。采用C-D生产函数，且假设规模报酬不变，则有如下观测方程：

其中，ΔLn(TFPt)为全要素生产率增长率，假设其为一个隐性变量，且遵循一阶自回归即AR(1)过程，则有如下状态方程：

ΔLn(Yt)＝ΔLn(TFPt)＋αΔLn(Kt)＋(1-α)ΔLn(Lt)＋εt　(3-15)

ΔLn(TFPt)＝ρΔLn(TFPt-1)＋ut　(3-16)

其中，ρ为自回归系数，满足｜ρ｜＜1，ut为白噪声。这样，利用状态空间模型，通过极大似然估计同时估算出观测方程(3-15)和状态方程(3-16)，从而得到全要素生产率增长的估算值。隐性变量法的最大优点在于，不再将全要素生产率视为残差，而是将其视为一个独立的状态变量。这样将全要素生产率从残差中分离出来，从而剔除掉一些测算误差对全要素生产率估算的影响。同时，在具体估算时，还充分考虑了数据非平稳性带来的伪回归问题。

(2)潜在产出法。

索洛残差法和隐性变量法在估算全要素生产率时，都暗含着一个重要的假设，即认为经济资源得到充分利用，此时，全要素生产率增长就等于技术进步率。换言之，这两种方法在估算全要素生产率时，都忽略了全要素生产率增长的另一个重要组成部分——能力实现改善即技术效率提升的影响。

潜在产出法正是基于上述考虑提出的，其基本思路是遵循法雷尔(Farrell，1957)的思想，将经济增长归为要素投入增长、技术进步和能力实现改善(技术效率提升)三部分，全要素生产率增长就等于技术进步率与能力实现率改善之和；估算出能力实现率和技术进步率，便给出全要素生产率增长率。^[39]

设Ry，t为产出增长率，RTP，t为技术进步率，CRt为能力实现率，Ryx，t为要素投入增长所带来的产出增长率，RTFP，t为全要素生产率增长率，则有：

且全要素生产率增长率等于技术进步率与能力实现率变化之和，即：(www.xing528.com)

能力实现率CRt测度了现有生产能力的利用程度，反映了现实经济的生产技术效率，通常利用产出缺口来度量。鉴于索洛残差法较为粗糙，所以通常利用隐性变量法估算的全要素生产率增长率作为技术进步率RTP，这样利用公式(3-18)便得到全要素生产率的估算。潜在产出法最大的优点在于，全面考虑了技术进步和能力实现改善对全要素生产率增长的影响，且借助这种方法可以更全面地分析经济增长源泉。但它的缺点也很明显，主要体现在它是建立在产出缺口估算基础上，而无论用何种方法估算产出缺口，都会存在估算误差，从而导致全要素生产率增长率估算偏差。

(二)中部地区TFP增长的估算

在上述方法中，我们将采用增长核算方法中的索洛残差法估算中部地区的TFP，主要原因有二：一是经济计量学方法测算TFP虽然可以放松增长核算方法中完全竞争市场和规模收益不变等假设，但是中部地区可用的统计数据量比较少，不能满足经济计量方法的数据要求。二是增长核算方法是国际上普遍接受的TFP测算方法，美国劳工统计局(BLS)从1983年开始公布用增长核算方法估计的美国TFP，选择索洛残差法有利于估计结果的国际比较。

1.估算方法与变量选择

运用索洛残差法，各投入要素的产出份额δn往往需要通过估算总量生产函数加以测算。具体估算中，常采用两要素(资本和劳动力)的C-D生产函数：，其中Yt为现实产出，Lt为劳动投入，Kt为资本存量，α、β分别为平均资本产出份额和平均劳动力产出份额。两边同时取自然对数有：

Ln(Yt)＝Ln(A)＋αLn(Kt)＋βLn(Lt)＋εt　(3-19)

εt为误差项，通常我们假设α＋β＝1，即规模报酬不变，则有回归方程：

Ln(Yt/Lt)＝Ln(A)＋αLn(Kt/Lt)＋εt　(3-20)

这是一个双对数模型，可以利用OLS估算。其中资本存量需要测算，按照永续盘存法测算公式为：

Kt＝It/Pt＋(1-δt)Kt-1　(3-21)

其中Kt为t年的实际资本存量，Kt-1为t-1年的实际资本存量，Pt为固定资产投资价格指数，It为t年的名义投资，δt为t年的固定资产的折旧率。在确定了资本存量的初值以及实际净投资后，便可以利用(3-21)式给出各年的实际资本存量。这样，利用回归方程(3-20)，我们可以估计出平均资本产出份额α和平均劳动力产出份额β，代入(3-14)式可以得到全要素生产率增长率。

在实际估算过程中，需要对基期资本存量、各年名义投资、固定资产投资价格指数和固定资产折旧率等相关变量进行确定与选择。

(1)基期资本存量K0。

对于基期资本存量的确定，通常采用直接推算的方法，如张军等(2004)对于基期的资本存量的确定采用1952年的固定资本形成除以10%得到，^[40]王志平(2010)也采用这个折算方法；魏下海(2009)对于各省份基期资本存量的估计，^[41]采取假定基期全国资本-产出比为3，然后假定某一省份占全国资本存量的比重与其占总GDP的比重相同，即可获得该省份1978年的资本存量。我们直接运用张军等(2004)的估算结果，确定1952年各省的基期资本存量。

(2)当年名义投资It。

对于当年投资I的选取存在着分歧，主要有三种观点：其一是采用积累的概念及相应的统计口径，其二是采用全社会固定资本投资，其三是采用资本形成总额或固定资本形成总额。张军等(2005)认为固定资本形成总额是衡量当年投资I的合理指标，^[42]单豪杰(2008)也持相同的看法。^[43]李宾等(2009)认为张军等采用的方法夸大了投资流量，其原因在于当期的投资额需在当期投入生产中，这样才能对当期的资本存量有贡献，因而采用新增固定资产指标更符合要求。我们对于当年投资的选取采用的是固定资本形成总额来表示。

(3)固定资产投资价格指数Pt。

郭庆旺等(2003)由固定资产投资价格指数乘以各省商品零售价格指数与全国商品零售价格指数的比值，得到我国各省份的固定资产投资价格指数。^[44]张军等(2005)的研究发现：在估算各个省份的资本存量时，对于1978年以前的投资价格指数采用统一的价格指数，而对于1978年以后的投资价格指数，各省应采用不同的价格指数而非统一的价格指数。因此，张军等(2004)采用固定资本形成总额及固定资本形成指数来构造隐含平减价格指数，作为实际固定资产投资的价格指数。我们采用张军等(2004)的方法，计算以1952年为基期的1996—2015年的实际固定资产投资的价格指数。

(4)固定资产折旧率δt。

对于折旧率的处理，为了与永续盘存法计算资本存量的方法一致，借鉴沈汉溪(2007)的做法，假定资本品的相对效率按照几何方式递减，采用几何效率递减的余额折旧法计算折旧率。张军等(2005)计算得到了各省固定资本形成总额的折旧率是9.6%，单豪杰(2008)在张军等(2005)的基础上，对我国的折旧率进行了重新估算，得出分省的估算中折旧率应为10.96%，我们选取的折旧率也为10.96%。

2.TFP增长的估算结果

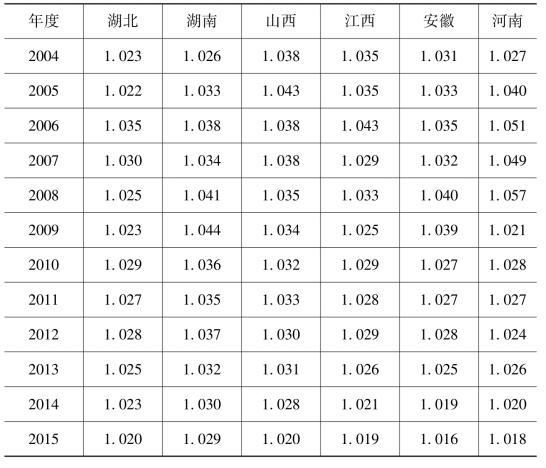
根据上述方法，在对基期资本存量、当年名义投资、固定资产投资价格指数和固定资产折旧率等进行确定与估算的基础上，运用永续盘存法的(3-21)式，计算1996—2015年中部六省的实际资本存量，结果见表3-4。

表3-4　中部六省实际资本存量的估算结果　　单位：亿元

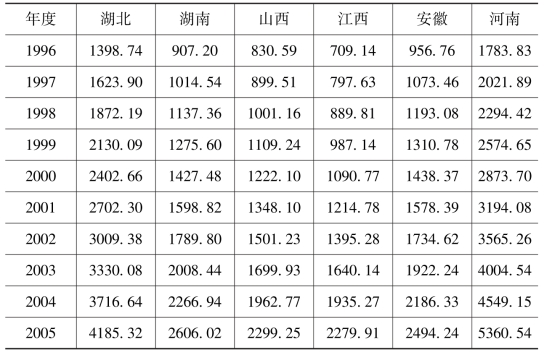
续表

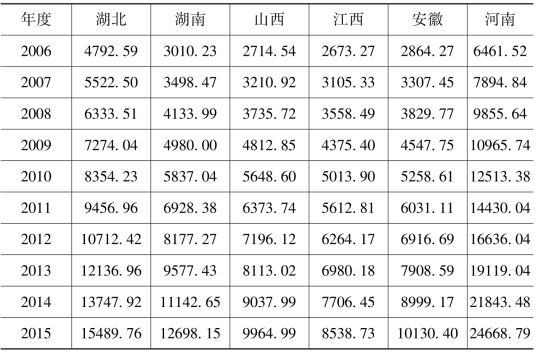
注：中部六省实际资本存量的估算以1952年为基期。

根据中部六省资本存量的估算结果和相关变量的数据，运用索洛残差法对中部六省TFP增长进行估计，结果见表3-5。

表3-5　中部六省TFP增长的估算结果

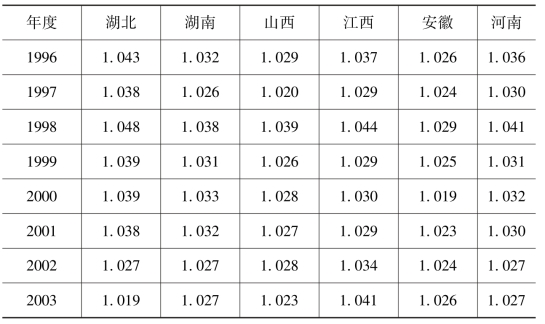
续表

根据表3-5中运用索洛残差法对中部六省TFP增长的估计结果，描绘1996—2015年中部六省及其平均TFP增长的变化趋势，见图3-5。

如图3-5所示，1996—2015年，中部地区平均TFP增长变化指数均大于1，说明全要素生产率呈现逐年增长的趋势。从总体上看，在此期间中部地区平均TFP增长呈现先下降(1996—2003年)，再上升(2004—2006年)，后下降(2007—2015年)的发展态势；其中，2009—2015年中部地区平均全要素生产率增长速度明显放慢，主要是受国际金融危机的不利冲击。就中部六省内部而言，在国际融危机期间，河南省TFP增长速度下降尤其显著，江西、湖北、山西也受到国际金融危机的不利影响，湖南、安徽受国际金融危机的冲击相对较小。

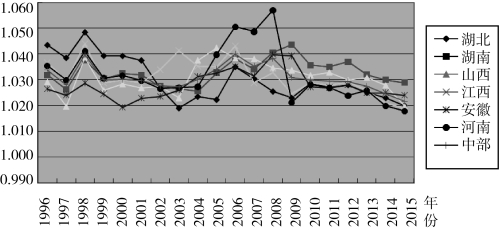
图3-5　中部六省TFP增长的变化趋势