行为资产定价模型的优化方法

1.BAPM 理论

1994年，席菲瑞和斯泰曼提出了行为资产定价模型（BAPM）。BAPM 是CAPM 的扩展。BAPM 模型认为市场上存在信息交易者和噪声交易者。信息交易者严格按照CAPM模型构建资产组合，噪声交易者则不会。他们会受到认知错误的影响，并且没有严格的均值方差偏好。两类交易者相互作用共同决定证券价格。当信息交易者在市场上占据主导地位时，市场是有效的；当噪声交易者在市场上起主导作用时，市场是无效的。

市场中同时存在信息交易者和噪音交易者具有十分重要的意义。设想市场中只存在信息交易者，对某只股票而言，所有交易者都能够对其进行精确分析，每个人对该股票的内在价值的认识都一致。因此，股票持有者只愿意在市场价格高于内在价值时出售股票，而潜在购买者只愿意在市场价格低于内在价值时购入股票，这就导致了股票价格永远维持在其内在价值上，并且不存在任何交易。可见，市场中存在不同的观点很重要，只有存在不同的观点，才会使得交易发生，由于噪音交易者对股票的估值没有严格的均值方差偏好，使他们对股票内在价值的认识有一定的偏差，从而让交易得以实现。

在早期的有效市场理论下，人们认为市场上的噪音交易者不能够长期存在，其原因是当噪音交易者使股票价格偏离其内在价值时，套利者便会出现并且迅速地将这一偏离纠正回应有的水平。然而，De Long、Shleifer、Summers和Waldman提出的DSSW 模型^[21]证明了噪音交易者实际上是可以获利的，甚至可能比理性交易者获利更多。噪音交易者得到的额外获利并非因为他们拥有更好的交易技巧，而是因为他们面临了更大的风险。噪音交易者承担的额外风险通常被称为“噪音交易者风险”（NTR，Noise Trade Risk）。由于噪音交易者并非按照有效信息进行交易，因此人为的非理性因素会造成一种新的不确定性。这种不确定性会继而影响到信息交易者，因为信息交易者往往无法得知噪音交易者会如何行动。因此，DSSW 模型指出噪音交易者由于承担了额外风险而能够赚取更多的钱。

更为重要的是，噪音交易者的存在会导致市场中的任一资产价格中都包含了噪音的因素，而这些噪音以及噪音交易者的行为会使得市场上存在噪音信号。当市场中噪音信号存在时，投资者并不能够很好地甄别有用信息和噪音，如上文所述，即便是信息交易者的估计也会存在偏差，从而形成了系统风险。除了基本风险以外，投资者还要承担噪音交易者风险（NTR），它可以被看作是噪音交易者的力量。噪音交易者的情绪是随机的，难以被理性交易者很好地预测。套利者是否进行市场出清，取决于噪音交易者的反应，但他们的反应是很难预测的。如果他们对市场看“牛”，他们将把价格推高到超出其内在价值（假设他们比套利者更有力量），以至达到他们想达到的程度。如果他们没有停止，意味着市场可能会变得疯狂。信息交易者也意识到他们面临着未知的风险要素。因此行为资产定价模型就要考虑这些错误，并在模型中消除噪音估计。

2.BAPM 模型

我们考虑这样一个金融市场，在金融市场中有H 个交易者，时间是离散的（t＝0，1，2，…，T）。新信息s在每一日期之初披露。在这里我们称s为某一状态，并假定s∈S＝{si}（S为有限集）；st ∈S表示在日期t被揭示的状态；xt＝（s0，s1，…，st）表示在日期t之初的公共信息。显然，这意味着，我们可以用树形结构来表示不确定性，反映到这里树形结构的节点为{xt}。不妨令si发生于日期t，sj发生于日期t+1，且从si到sj的变换由变换矩阵为∏＝∏ij的不可约马尔可夫链决定。

在日期0之初，交易者h所持有的初始组合为wh。如果h持有组合wh 到日期t，且在日期t之初的公共信息为xt，那么h在日期t所获得的股利为wh（xt）。在这里我们用符号w＝∑h wh 表示市场组合。日期t+1的马尔可夫状态s决定了股利增长率w（xt+1）/x（xt）。对每一状态s而言，根据特定变换分布Prob{w（xt+1）/w（xt）|s}将S分解为子集{sw}。在这里，我们把sw 称为在状态s条件下股利增长率的充分统计量。

用向量Z＝[Z（xt）]表示证券，其中Z（xt）为一单位证券在状态xt支付给投资者的回报数量。我们假定，证券市场所提供的证券集合非常丰富，从而使证券市场具备完全市场特征。因此，存在状态原函数来决定证券价格。令r（xt）表示xt—状态或有要求权的价格，且r＝[r（xt）]。不妨取x0为计算单位，那么有：r（x0）＝1。由此可见，在日期0的市场上，证券Z＝[Z（xt）]的价格qz（x0）为r·Z；而在状态xt 的市场上，证券Z的价格qz（xt）为r′（xt）·Z/r（xt）。

事实上，分析噪音交易者对特定证券集的影响，是本节所主要研究的内容之一。我们假定在每个日期t，这些证券都是可交易的。这些证券集包括：（1）零息票、无风险债券。这两种债券是构成利率期限结构的基础。我们假定，到期日为t的零息票债券在日期t之前都可以进行交易。（2）市场组合。市场组合用符号Zw 表示，且为w 的实量倍数。（3）市场组合的买权与卖权。以状态xt 发行的买权执行价格为K、到期日为t+j、回报为max{qw（xt+j）－K，0}，其中qw（xt+j）表示市场组合在xt+j—市场状态的价格。卖权与买权类似，不同之处在于其回报为max{0，K－qw（xt+j）}。(www.xing528.com)

在日期t之初，交易者的财富由两部分组成：（1）xt－1 状态下所持有的组合市值；（2）xt状态下的股利支付。此后，交易者将xt状态下的财富分成两部分，一部分用于t期的消费，另一部分用于储蓄。储蓄部分投资于证券，并构成该交易者在xt 状态下的组合。用符号zh（xt）表示交易者h的xt—或有商品的净交易额，那么，消费向量ch＝[ch（xt）]可表示为：ch＝wh+zh。

另外我们用过程{xt}的概率分布Ph 表示交易者h的主观信念。在这里，对数效用对描述长期交易者生存具有非常重要的意义。在BAPT框架里，交易者都具有贴现率为正的对数效用。不仅如此，消费计划ch 的设定一般是通过在生命周期预算约束r·zh≤0条件下最大化期望效用EUh 来进行的。通常，交易者h的跨期效用函数可表示为：

式中，γh＜1为交易者h的时间贴现因子。假定效用期望函数EUh 表示交易者在状态xt下的偏好选择，在这里，期望值EUh 是在主观概率分布Ph 的基础上求得的。

为获得均衡状态原函数r，不妨考虑交易者h期望效用的最大解。定义：

在r·zh ≤0条件下最大化EUh，由此可得交易者h的需求函数：

式中，Wh 为交易者h的市场财富r·wh。在BAPT框架里，方程（5-3）是确定对数效用最大值的重要条件。值得注意的是，该条件中的或有要求权预算份额可反映交易者h的主观信念。

事实上，我们可用条件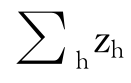（r）＝0来定义均衡状态原函数r。我们知道，在BAPT框架中，价格的作用在于将交易者的信念与贴现函数汇聚到代表性交易者的信念与贴现函数中。因此，在这个意义上，通过分析噪音交易者对代表性交易者信念的影响，就可以确定噪音交易者对市场的影响。

在这里，我们用概率{Γ（xt）}及贴现因子{γtR}表示代表性交易者。概率{Γ（xt）}通常可按如下方式确定，即令ωh 表示交易者h的相对财富份额Wh/∑j Wj（其中j＝1，2，…，H），那么概率Γ（xt）就可表示为交易者的主观概率的凸组合∑hδh Ph（xt），其中，。另外，贴现因子γR（t）t 可用∑hωhγth 定义。在此基础上，就可直接确定r的原函数，即：