提起美国基础教育的课程,不得不提的就是《州共同核心标准》。对于数学而言,从幼儿园到初中8年级,都是按照“年级”列出了数学课程的标准。而到了高中(9—12年级),《州共同核心标准》使用“概念类别”的方式提出标准,这些概念的类别包括:数与数量,代数、函数、建模、几何、统计与概率。
虽然说不是所有州都在严格执行《州共同核心标准》,但不可否认的是,它还是起到了相当强的指导作用,各州如果制定了自己的标准,州的标准只会比《州共同核心标准》的要求更高。从效果来讲,幼儿园到初中对各州学校的约束力更高,也更加容易接受,而因为高中有了各类与大学入学相关的标准化入学考试、学校的课程大纲要求更高等原因,高中部分的《州共同核心标准》基本上只有象征性的指导意义。尽管如此,《州共同核心标准》能够帮助我们了解美国基础教育阶段数学的大致要求。
值得注意的是,在比较通用的IXL[10],可汗学院等学习网站上,都是按照《州共同核心标准》的要求整理了各类视频和题库。
表5-4 可汗学院网站列出的课程图
(续表)
小学和初中是高中数学课程和教学的起点,对小学和初中阶段的课程和教学进行了解,有助于我们了解高中阶段的数学课程和教学。
(1)小学与初中
8年级对于美国来说,是初中阶段的结束,而对于国内课程来讲,对应的是初中二年级,还有一年才是初中毕业。下文把这个年级段的中美两国学生学习内容做个简单比较,从而对两国的小学和初中阶段的数学课程有个初步印象[11]。上海市8年级数学课程的主要知识点(部分)包括:
①二次根式
二次根式的概念和性质;最简二次根式与同类二次根式;二次根式的运算;一元二次方程的概念;一元二次方程的解法;一元二次方程的判别式;一元二次方程的应用;等等。
②正比例和反比例函数
函数的概念;正比例函数;反比例函数;函数的表示法;等等。
③几何证明
命题和证明;证明举例;逆命题和逆定理;线段的垂直平分线;角的平分线;轨迹;直角三角形全等的判定;直角三角形的性质;勾股定理;两点间距离公式;等等。
④一次函数
一次函数的概念;一次函数的图像;一次函数的性质;一次函数的应用;等等。
⑤代数方程
一元整式方程;二项方程;可化为一元二次方程的分式方程;无理方程;二元二次方程和方程组;二元二次方程组的解法;列方程(组)解应用题;等等。
⑥四边形
多边形;平行四边形;特殊的平行四边形;梯形;等腰梯形;三角形、梯形的中位线;平面向量;平面向量的加法;平面向量的减法;等等。
确定事件和随机事件;事件发生的可能性;事件的概率;概率计算举例;等等。
美国《州共同核心标准》针对8年级数学课程的内容主要体现在以下方面:
①数系
知道有些数字不是有理数,并用有理数近似它们。
②表达式和方程式(https://www.xing528.com)
使用根号和整数次方;了解比例关系,直线和线性方程之间的联系;分析和求解线性方程式和联立线性方程组。
③函数
定义,评估和比较函数;使用函数为数量之间的关系建模。
④几何
使用物理模型,透明胶片或几何图形软件了解全等和相似;了解并应用勾股定理;解决涉及圆柱,圆锥和球体体积的现实世界和数学问题。
⑤统计和概率
研究双变量数据中的相关性规律。
如果结合两国相应年级相关的学生数学学习和教师教学材料做一些粗浅的比较和分析,我们可以发现:上海的课程严谨、逻辑性强,为学生打下了扎实的基础;美国的课程内容简单,不追求严谨,强调了对概念的理解和与实际生活的联系。因这一部分不是本书的重点内容,不再作深入的对比和分析。
海量的信息化资源为美国当地学生的个性化学习奠定了基础。下面便是两个例子。
可汗学院根据《州共同核心标准》录制了很多小视频,帮助学生学习数学,另外还设计了练习、测验、积分等各类“玩法”帮助用户坚持学习并了解自己学习的质量。
IXL在《州共同核心标准》的下面还进行了更细的划分,并把各类考察的题目进行了相应的归类,从而有助于了解学生在各知识点和技能的掌握情况与进度。
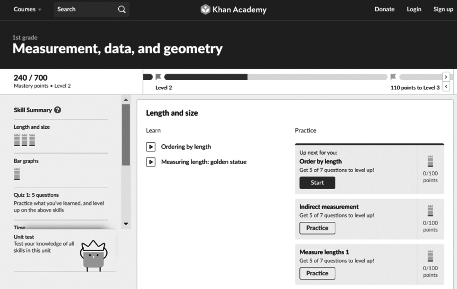
图5-1 可汗学院1年级数学科目学习界面

图5-2 IXL在8年级数学州共同核心标准下进行细分
(2)高中
无论是公立还是私立高中,数学课程分为不同的水平(或是难易度不同的课程)供学生选择。据笔者初步的观察,公立学校的分层教学更为明显和多元,这可能与公立学校不选拔生源相关。
基于学校师资力量和资源,学校课程内容会有很大的不同。另外,学校一般都会开设各种不同层次和内容的课程,供学生根据自己的能力和兴趣进行选择。就高中学段来讲,国内的数学课堂内容的深度、严格性可以说“远超”美国的普通数学课堂。但是,美国的大部分高中也会提供一些难度比较高的课程或者高等数学的课程,特别是那些选拔性的学校。下面给出两个例子。
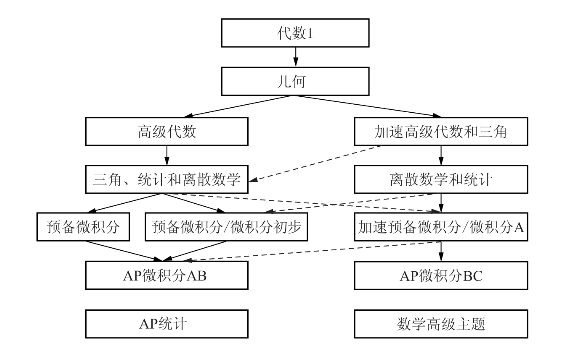
图5-3 芝加哥大学附属实验学校数学选课路径图[12]
芝加哥大学实验中学的高中数学课程包括:代数、几何、高级代数、加速代数和三角学、离散数学和统计、加速微积分初步、三角、统计与离散数学、微积分基础、AP微积分AB、AP微积分BC、数学中的高级内容,等等。另外,如果学生在AP微积分BC考试中获得满分,即可申请参加芝加哥大学数学系的分班测试,根据测试结果安排到芝加哥大学数学系与数学系学生一起修习大学数学的内容。图5-3是芝加哥大学实验学校高中数学课程选课路径图。
在伊利诺伊数理高中(IMSA),提供的数学课程包括:几何、数学探究系列、微积分系列。其中,数学探究系列主要在9—10年级展开,目的是为后续的数学学习打好基础,帮助学生养成探索数学问题的良好习惯,形成适合自己的方法。微积分系列主要以AP课程为主。在满足一些基本要求(完成前置课程)的前提下,可以选修一些大学数学的基础课程,包括:离散数学,统计探索与描述,统计实验与推断,现代几何,数论,微分方程,多元微积分,线性代数,分析理论,等等。

图5-4 伊利诺伊数理高中数学选课路径图[13]
伊利诺伊203学区是个公办学区,它不仅提供了高中阶段的基础课程,也提供了丰富的大学水平的课程供学生选择,比如,多元微积分、线性代数、量化素养(为进行研究准备的一门研究统计方法与数据分析的课程)。

图5-5 203学区高中学段所用的数学教科书
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




