在进行教学设计时，有时故意“诱敌”深入，激发学生的兴趣，磨砺他们的意志，从而孕育学生的数学素养。比如问题三（6）中提出关于“最小二乘法”是否使得“横向距离”同时达到最小，笔者在教学过程中故意给学生挖了两个“坑”。
命题：既然线性回归模型使得
达到最小，那么
也能同时达到最小，理由如下：
既然
达到了最小，根据上式，
也达到了最小。
这个“坑”还不容易被发现。能够正确对其进行辨识的学生，数学素养还是不错的。如果学生能够更进一步给自己的想法佐证，那数学素养就更高了。
事实上，对于
要使得
达到最小，那么有：
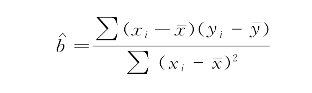
如果以x为应变量（responsive variable），假设回归模型为x＝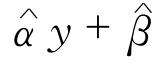
，那么要使
为最小，则应有
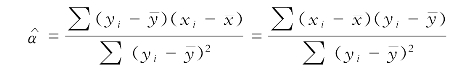
从而转化成y为应变量时，
，从而，
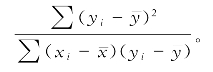
问题来了：如果原回归模型
使得“横向距离”同时保持最小，那么
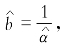，也即：
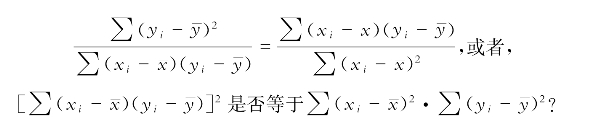
此时，可以再次“诱导”学生：看似不合情理的等式，在“最小二乘法”背景下，的确可能是成立的，比如，问题二（1）、（2）、（3）都看起来那么“巧合”，特别是前文已经证明了的问题三（2）中的如下两个等式：
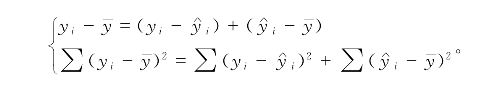
怎么办？反应迅速的学生可能想到用数据首先进行验证，从而打消疑虑，毕竟进行数据验证可能比证明来得迅速，避免“无用功”。
表3-14 使用Excel验证“猜想”（2）
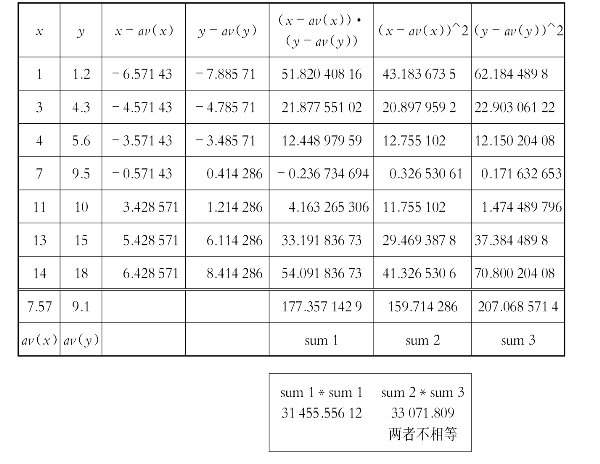
从而知晓，使得“纵向距离”最小的回归直线并不能使得“横向距离”同时最小，这与第二部分中使用技术后验证等式成功的感知不同。必须指出的是，前述推导过程对思辨、抽象等能力和素养有较高的要求。
同时，以上问题的初步解决又带来了一个“新”问题：使得“纵向距离”最小和“横向距离”最小的回归直线不是同一条，那么两者有关系吗？这在本节第一部分：技术“探路”，数字“说话”中已经有了解答。
从本节内容可见，一元线性回归这一单元既充满了应用的色彩，又有着充分严格的数学推理和证明作为支撑；既能够激发学生应用数学的兴趣，又能够培养学生严谨的数学思维。它是一个值得花力气研究其教学设计的好题材。
【注释】
(www.xing528.com)
[1]http：//m.mamicode.com/info-detail-2193551.html.
[2]bbs.zol.com.cn.
[3]www.qnong.com.cn.
[4]www.leyijc.com.
[5]dp.pconline.com.cn.
[6]Self-avoidance and Tiling：Mechanisms of Dendrite and Axon Spacing，Wesley B.Grueber and Alvaro Sagasti.
[7]Self-avoidance and Tiling：Mechanisms of Dendrite and Axon Spacing，Wesley B.Grueber and Alvaro Sagasti.
[8]Michael Haese，Mark Humphries，Chris Sangwin，Ngoc Vo，Mathematics Applications and Interpretation 2［M］.Australia：Haese Mathematics，2019.
[9]www.huahuibk.com.
[10]www.fraps.com.
[11]测试题改编自Applications and Interpretation，Haese Mathematics.
[12]张金磊，王颖，张宝辉.翻转课堂教学模式研究［J］.远程教育杂志，2012.（4）46—51.
[13]中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社）.
[14]https：//app.kognity.com/schoolstaff/app/ibdp-mathematics-applications-and-interpretation-hl/book/probability-and-statistics/confidence-intervals.
[15]https：//app.kognity.com/schoolstaff/app/ibdp-mathematics-applications-and-interpretation-hl/book/probability-and-statistics/confidence-intervals.
[16]中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2018.
[17]Michael Haese，Mark Humphries，Chris Sangwin，Ngoc Vo，Mathematics Applications and Interpretation 2［M］.Australia：Haese Mathematics，2019.
[18]https：//www.khanacademy.org/computing/computer-science/informationtheory/moderninfotheory/v/markov_chains以及https：//www.khanacademy.org/computing/computer-science/informationtheory/moderninfotheory/pi/markov-chain-exploration.
[19]Origin of Markov Chains［EB/OL］.https：//www.khanacademy.org/computing/computer-science/informationtheory/moderninfotheory/v/markov_chains
[20]Markov Chain Exploration［EB/OL］.https：//www.khanacademy.org/computing/computer－science/informationtheory/moderninfotheory/pi/markov-chain-exploration
[21]吴军.数学之美［M］.北京：人民邮电出版社，2014.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
