技术探路：数字说话的新趋势

对于问题一（2）和问题三（3），设计了一道学生动手操作的探究题，让“数字”直接“说话”，加深直观理解。探究步骤如下：

1.阅读表3-5中给出的数据：

表3-5　原始探究数据

2.使用计算器计算相关系数r1，写下回归直线的方程y＝m1x＋n，其系数和常数都完整保留所有计算器给出的数值，下同。

3.对表3-5中的x，y数据都实施如下线性变换：乘以3加上2。完成下表3-6：

表3-6　探究数据变换1

4.为表3-6中的数据计算相关系数r2，同时写下回归直线的方程。

5.对表3-5中的x，y数据都实施如下线性变换：除以2减去1。完成下表3-7：

表3-7　探究数据变换2

6.为表3-7中的数据计算相关系数r3，同时写下回归直线的方程。

7.从以上计算中，发现了什么规律？

8.把表3-5中的x值除以3加4，保持y值不变。把新的数据填入表3-8。

表3-8　探究数据变换3

9.为表3-8中的数据计算相关系数r4，同时写下回归直线的方程。

10.你发现了什么规律？如果需要的话，模仿第8步的方法自行采集另一组数据进行分析。(www.xing528.com)

11.把表3-5中的y值乘以2减去2，保持x值不变。把新的数据填入表3-9。

表3-9　探究数据变换4

12.为表3-9中的数据计算相关系数r5，同时写下回归直线的方程。

13.你发现了什么规律？如果需要的话，模仿第11步的方法自行采集另一组数据进行分析。

14.为表3-5中的x，y值分别计算标准差Sx和Sy。

15.分别计算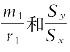的值。你发现了什么？

16.互换表3-5中x，y的值，为新的数据计算相关系数r6。r6和r1有什么关系吗？如果需要，可以自己寻找一组数据重复同样的操作以寻找线索。为这组数据计算线性回归方程y＝m6x＋b。分别计算m1·m6and r1·r6的值。你发现了什么？与第15步中的结论比较。

17.使用表3-5中数据的回归直线方程y＝m1x＋n计算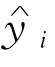，并将数值均填入下表3-10。

表3-10　探究数据回归值

分别计算Var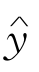（）和Var（y）的值，从而计算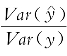，比较它与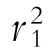的关系。你发现了什么？

通过上述17个步骤的实验，学生对于变量的关系及相关统计量的性质有了直观的印象，接下来教师可以对于相关系数r和线性回归为何有这些规律进行进一步的数学探究。

在上述实验中，反复使用了图形计算器或其他技术实现回归方程的计算等。在统计中，Microsoft Excel有时也是一个强有力的技术工具。比如，Excel表3-11初步验证了问题三（2）中的等式：。

表3-11　使用Excel验证恒等式

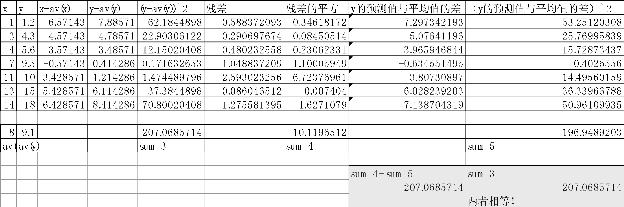
表3-12　使用Excel进行回归分析

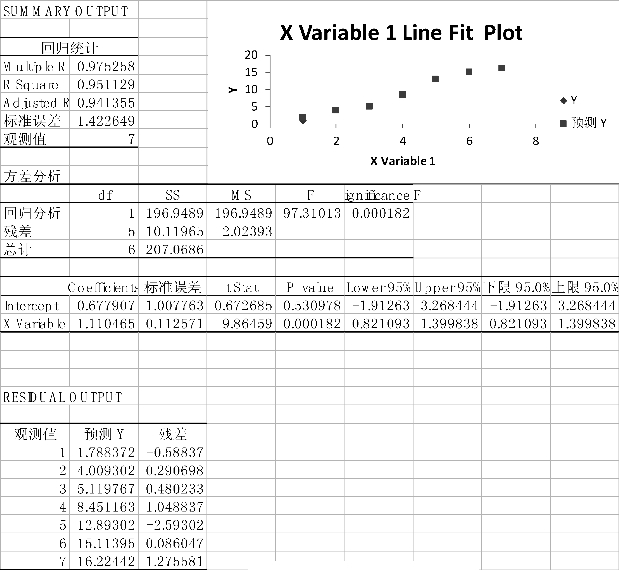
Microsoft Excel的回归分析功能也是很方便学生进行使用的，能够体现一定的数字素养，表3-12便是由Excel输出的表3-11数据的一元回归分析。