一元线性回归的重要知识点及影响因素

一元线性回归是统计课程中一个基础知识点，它不仅有严密的数学推导，也有重要的应用，对于初步理解统计学科的原理、概念和方法可起奠基作用。它不仅出现在AP统计课程、IB数学课程、A-Level数学课程等国际课程中，也出现在我国《普通高中数学课程标准（2017年版）》中。在实际学习中，因为回归直线等相关结论非常简洁、优美，有的结论与直观感受非常“一致”或明显“冲突”，学生不由得会对一些看似“巧合”的结论的来源感到好奇，而在数学课中满足学生的好奇心非常必要。

本节并不是就一元线性回归这一单元介绍其完整的课堂教学设计，而是试图理一理这个单元中需要帮助学生厘清的重要知识点。对于其中部分知识点，笔者设计了一些结合数据的实验或命题证明，引导学生处理和分析数据或者进行数学推导，从而帮助学生获得一些进行科学研究的直观感受，从而加深认知，促进深度学习和数学素养的培育。

在本单元的教学设计中，教师需要解决的问题包括（但不限于）：

问题一

（1）相关系数相关公式的来源和相互关系：

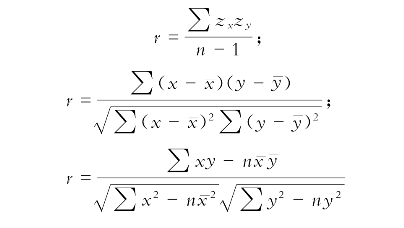
（2）交换x，y的值后，相关系数r是否产生变化？对x，y各自进行线性变换（可以是不同的线性变换）后，相关系数r是否受到影响？在上述两种变换的情况下，线性回归直线的斜率各自受到什么影响？

问题二

（1）如何使用“最小二乘法”得到回归直线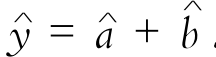x，其中

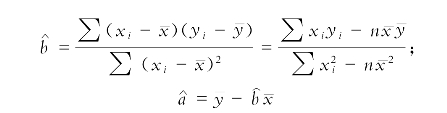
从而帮助学生知晓为何回归直线一定会通过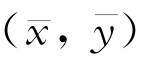这个特殊点。

（2）学生一定想知道为什么下式成立：

(www.xing528.com)

（3）学生一定还想知道是否成立。

问题三

（1）判定系数（coefficient of determination）的公式是如何推导出来的，为何它就“恰巧”等于相关系数的平方（r 2）？

（2）r2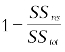＝，这里SSres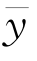＝）2，并且“恰好”有SStot－SSres＝，而这又似乎与yi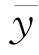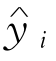，，的三角关系恒等式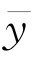yi－＝（yi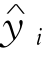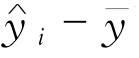－）＋（）有着某种联系。是什么联系呢？

（3）“r 2为判定系数，它可以解释yi的变差在多大程度上是由线性关系产生的。”这种说法的数学根据是什么？事实上，可以推导出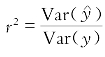，从而帮助学生进行理解。

（4）是否r越靠近1，所使用的线性模型就是越合适的？事实上，评价一个线性模型是否合适，除了需要考虑原始散点图、判定系数r 2外，还要考虑残差图。

（5）在回归分析和假设检验中，原假设是“没有线性关系”，当p值低于显著水平时，结果显著，而当｜r｜大于临界值时，结果显著。为什么？

（6）在使用“最小二乘法”时，我们得到的拟合直线使得“纵向距离”（残差平方和，也即最小，那么所得到的拟合直线是否同时使得“横向距离”，这里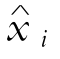指把yi代入拟合直线后得到的x的值）最小呢？

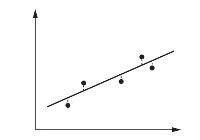
图3-36　“纵向距离”示意图

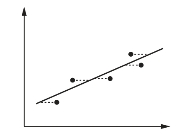
图3-37　“横向距离”示意图

下文介绍笔者在实际教学中对上述部分问题的教学做法，与读者商榷。