教学设计：引起学生兴趣的新冠病毒Covid-19传播假设

教师设计三个与学生学习或生活息息相关的场景，增强学生的“代入感”。同时，让学生成为课堂的“探究”主体，教师仅起“穿针引线”的作用，帮助学生在原有数学知识的基础上发展数学知识点之间的联系。就“马尔科夫链”而言，矩阵运算、矩阵的特征值、特征向量、解方程组、条件概率、树形图、极限等基础知识点全部串联了起来，是一种很好的数学探究课设计素材。

2.1　第一场景：午餐选择

从学校生活出发，探讨学生中午选择在学校餐厅吃饭（是）还是选择其他方式吃饭（否）各自的概率。经调研得知：

P（明天在餐厅吃饭｜今天在餐厅吃饭）＝0.9

P（明天在餐厅吃饭｜今天不在餐厅吃饭）＝0.15

要求学生完成绘制如下的树形图：

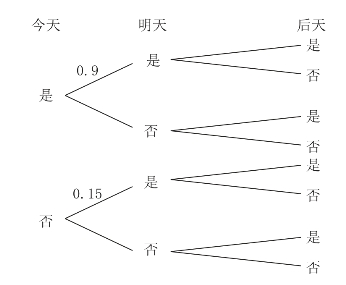
图3-27　是否在餐厅吃饭树形图

2.2　独立求解

教师要求学生独立求解如下四个结果：

P1（后天在餐厅吃饭｜今天在餐厅吃饭），

P2（后天不在餐厅吃饭｜今天在餐厅吃饭），

P3（后天在餐厅吃饭｜今天不在餐厅吃饭），

P4（后天不在餐厅吃饭｜今天不在餐厅吃饭）。

当学生求解以上结果时，要求学生保留原始过程。同时，教师引导学生总结出，第n＋1天的可能状态的概率分布仅取决于第n天的概率分布，与第1天到第n－1天的状态均无关。此时，教师逐渐引出马尔科夫链的定义，并指出这个特性便是马尔科夫链的定义来源。

设计意图：从学校生活出发，快速抓取学生对于本堂课的兴趣。树形图是概率中的基本知识点，独立绘制有助于学生温故而知新。这部分知识是以往学习过的，因此要求学生进行独立求解。要求学生保留原始过程是为了帮助学生与接下去转移概率矩阵的运算取得联系。

2.3　概念介绍

教师使用第一场景向学生介绍“马尔科夫链”和“转移概率矩阵”的概念。下面的矩阵就是此问题的“转移概率矩阵”的结果，其中“是”表示在学校餐厅吃饭；“否”表示不在学校餐厅吃饭。

同时，师生一起绘制“转移状态图”如下：

图3-28　是否在餐厅吃饭转移状态图

2.4　继续使用第一场景

假设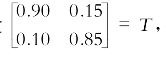要求学生进行小组合作，计算T 2，T 3，比较上述条件概率与计算过程，从而与“转移矩阵”相联系，同时要求学生总结T n的意义。

设计意图：矩阵的计算依赖于图形计算器或网络计算器或软件，通过分组合作，帮助学生实现“同伴学习”。在活动中，学生学会归纳、总结和解释。

2.5　引入第二场景：天气

考虑“晴朗”“多云”“下雨”三种天气状态，给出“树形图”如下（数据故意有所缺失），请学生分组绘制“转移状态图”和“转移矩阵”。

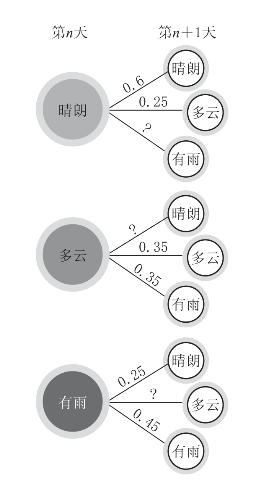
图3-29　天气情况转移状态图

学生能够绘制如下转移状态图和转移矩阵：

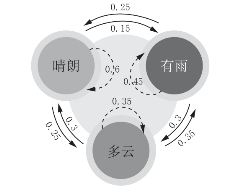
图3-30　天气状况转移状态图

接下来，要求学生进行小组合作，计算P 2，P 3，比较上述条件概率与计算过程，从而与“转移矩阵”相联系，同时要求学生总结P n的意义。

设计意图：帮助学生巩固转移状态图和转移矩阵的概念，同时从“二元”过渡到“三元”，对部分同学可能具有挑战性，故继续采取分组合作的办法。同时，绘制“转移状态图”与作图有关，学生容易感到好奇和兴奋，充分调动积极性。

2.6　为了进一步引起学生的兴趣，教师引入第三个场景：新冠病毒Covid-19的传播

假设新冠病毒Covid-19的传播的转移状态图（数据故意缺失）如下：请同学们独立完成其转移概率矩阵，结果如下：

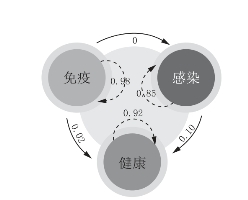
图3-31　Covid-19传播转移状态图

(www.xing528.com)

要求学生进行小组合作，计算S 2，S 3，通过比较上述条件概率与计算过程，从而与“转移矩阵”相联系，同时要求学生总结S n的意义。

设计意图：新冠病毒的传播是传染病历史上的一个大事件，所有学生都印象深刻。借此机会，让学生体会：身边有很多现象可以通过数学模型来模拟和解释，以激发学生学好数学的内生动力。同时，学生思考与构造矩阵的同时，能够结合当今疫情传播的一些常识发展自己对数据的理解，也帮助他们关心社会和公共卫生事件。

以上，已经把条件概率和树形图进行了复习，同时把“转移状态图”和“转移概率矩阵”进行了讲解和练习。通过小组活动和学习，同学们理解了通过利用树形图计算概率和利用“转移概率矩阵”进行计算所得结果的关系。接下来，课堂将把重心放在转移概率矩阵的“稳定状态”的探究上。

2.7　以小组为单位探讨

各小组任意选择场景1：餐厅吃饭；场景2：天气预报；场景3：新冠病毒传染。

2.7.1　对于场景1：假设学校有900名学生，第一天有852名选择餐厅吃饭，48名选择不在餐厅吃饭。使用T作为概率转移矩阵，请分别预测3天、10天后选择在餐厅和不在餐厅吃饭的人数。

对于场景2：假设今天晴天、多云和下雨的概率分别是0.2、0.6和0.2。使用P作为概率转移矩阵，请分别预测3天、10天后晴天、多云和下雨的概率分别是多少。

对于场景3：新冠疫情背景下，假设目前一个小镇上有99.4%的人口是健康状态，0.3%是感染状态，0.3%是免疫状态。使用S作为概率转移矩阵，请分别预测3天、10天后健康、感染和免疫状态的人数分别所占的比例。

这一任务要求学生进行组内的个人独立探究。

2.7.2　要求学生使用合适的技术分别计算T 50，T 100，T 150，T 200；P 50，P 100，P 150，P 200；S 50，S 100，S 150，S 200等，阐释它们的意义，同时询问：是否发现了什么规律，可以总结一下吗？这一任务要求学生进行小组共同讨论探究。

2.7.3　对于各个场景，请同时使用2.7.1中给出的数据和自己任意编造的初始数据，通过2.7.2中的结果，计算不同的终了状态。这一任务要求学生进行独立探究，并且询问：是否发现了什么，可以总结一下吗？

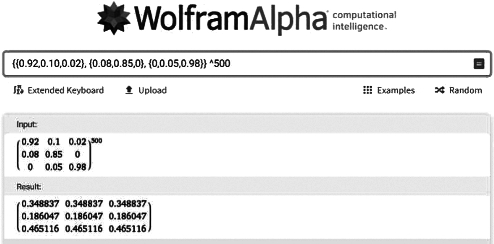
图3-32　场景3的稳定状态探究

设计意图：通过小组合作或独立探究的计算体验，帮助学生理解马尔科夫链的“稳定”状态。这个结果不是由教师直接给出，而是由学生经历一遍计算的过程然后得出。这些计算显然并不适合手动计算，需要学生使用图形计算器或类似Wolfram Alpha之类的网络计算器，或者Matlab等专业数学软件进行计算。它同时对于学生基于概念的理解有一定的要求。在得出结果的时候，学生普遍的反映是比较惊讶的，这会更加激发他们追问“为什么”，好奇心被激发，对数学的兴趣得到鼓励，数学应用的意识也得到提高。

具体来讲，2.7.1的设计主要是“热身”效应，学生进行初步的计算后，理解运算的结果并能够进行解释。场景1和场景2、3的不同之处在于，场景1使用的是具体的数字，而后两者使用的是百分比或概率。这会在何种程度影响结果呢？引发学生的思考。2.7.2的设计是帮助学生找到“稳定状态”，同时通过小组讨论的形式，让学生互相启发，共同探究。教师也可以询问启发性的问题，比如，对场景1，可以询问学生：既然0.15＞0.10，在学校餐厅就餐人数是否会一直增加下去？对于场景2：既然0.15＜0.25，是否晴朗的概率越来越大呢？对场景3，可以询问：既然0.08＜0.1，是否感染人数的比例最终为零？2.7.3的提出是基于前面学生已经尝试了不同的初始数据的使用，由学生使用自己“编造”的数据各自独立完成可以帮助学生理解：最终状态与初始数据是否有关？

2.8　从“应用”中回归，逐步抽象出“稳定状态向量”和“长期概率矩阵”的概念

实现方法：使用场景1，向学生讲解如何使用解二元一次方程组的方法计算出“稳定状态向量”。期间，带领学生复习方程组的解法，特别是无穷多解的解法，矩阵的特征向量、特征值等知识点同时得到复习和巩固。与此同时，充分使用图形计算器或其他工具进行方程组的求解。

例题1：假设学校有900名学生，第一天有852名选择在餐厅吃饭，48名选择不在餐厅吃饭。转移状态图如下：

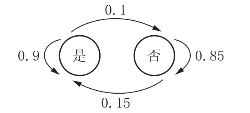
图3-33　是否在餐厅吃饭的转移状态图

请给出稳定状态下多少人在餐厅吃饭，多少人选择不在餐厅吃饭。

如果第一天有300名选择在餐厅吃饭，600名选择不在餐厅吃饭，使用同样的马尔科夫链后，结果有变化吗，有什么不变的吗？

例题2：新冠疫情背景下，假设目前一个小镇上有99.4%的人口是健康状态，0.3%是感染状态，0.3%是免疫状态。转移状态图（部分数据缺失）如下：

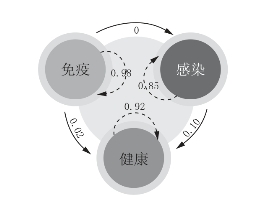
图3-34　新冠疫情转移状态图

请给出稳定状态下各有多少比例分别处于健康、感染和免疫状态。

如果刚开始有100%的人口处于健康状态，使用同样的转移状态图后，结果有变化吗？

设计意图：学生已经在先前的活动中比较熟悉两道例题所涉及的场景，这样设计的目的是给学生完整“代入”各类场景，省去课堂上不断熟悉新场景和输入新数据的时间，把省下来的时间用于更有意义的对问题的探究。通过这两道例题，一方面巩固“稳定状态”的知识，另一方面，把马尔科夫链相关内容与矩阵的运算、多元一次方程组（主要是二元和三元）无穷多解的解法等基础知识点结合了起来，学生感受到高中数学知识中基础部分的意义。

2.9　练习环节

配置与例题相似的题目供学生练习，此处略。

设计意图：帮助学生适当巩固两个例题中所学到的基本知识和技能。

2.10　带领学生一起思考场景3

这个模型是否有可以改进的地方？做一些探究。这个环节采取全班集体讨论的形式。事实上，一般病毒（如普通流感）感染的死亡率很小，因此大部分传染病模型并不会考虑死亡。但真实情境下，疾病在现实中会有一定的死亡率。如果我们改进原有的三阶模型为四阶的情况：

设计意图：学生使用技术进行探究时，会遇到困难，因此不免会发出疑问：“为何迟迟不收敛”？事实上，这个模型很难稳定（意味着在n取得相当大的值的时候才会稳定）；同时，普通计算器可能并不能承载这么大的计算量，需要使用高级一些的软件或网络计算器才能实现。同时，借用转移状态图，教师可以讲解为何出现“死亡”一栏后，最终的稳定概率矩阵结果会呈现为：

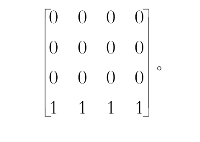
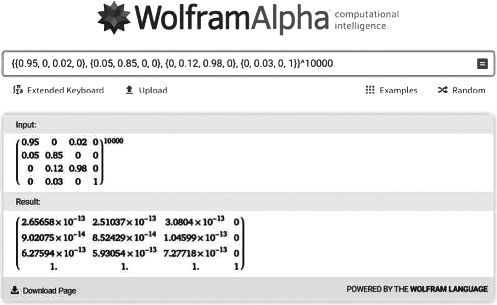
图3-35　场景3引入“死亡”后的稳定状态探究

通过这些尝试，发散学生的思维，引导他们更深层次地去考虑马尔科夫链问题，学有余力的同学可以进一步挖掘其原理和应用。

以下是一些可供学生深入研究的话题：以二阶概率转移矩阵为例，它为何会收敛到稳定状态呢？喜爱研究数学的高中生对此给出严格的证明也是有可能的。马尔科夫链除了在传染病传播模型上有着广泛的应用，还有什么其他的应用呢？马尔科夫链是如何被人们发现（或发明）的呢？教师可以提供可汗学院的两个短视频^[18]供学生作为课外参考资料。对于爱好计算机科学特别是语音识别技术和机器学习的同学来讲，可以阅读一些隐含马尔科夫模型的材料，等等。