优化小学入学问题的教学实施策略

2.1　课前准备

教师使用Blackboard平台创设论坛，要求学生回顾“中心极限定理”；给出在线应用程序进行虚拟实验的链接；同时提出一系列引导性问题。

设计问题如下：

问题一：将样本大小n设置为10，并生成100个随机样本

回答以下问题：

1.当提高置信水平时，置信区间将如何变化？

2.当置信水平设置为99%时，有多少区间不包括总体平均数？

3.当置信水平设置为95%时是什么结果？90%呢？

4.讨论更改样本大小时，置信区间发生的变化。

5.使用以上步骤的发现，描述样本数量和置信度水平对置信区间的影响。

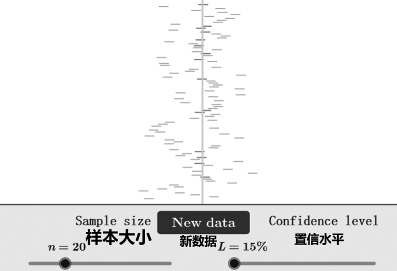
图3-24　模拟置信区间实验^[14]

问题二：基于概念的理解

学习物理专业的大学生在学习生涯的早期就会不停地接触“不确定性”的重要性。麻省理工学院的物理学教授Walter Lewin曾经有过一句话很好地描述了这一点：“任何没有对其不确定性的认知的度量是毫无意义的”。使用样本均值对总体进行预测时，了解物理学和其他学科中样本均值的不确定性至关重要。说说你的发现。

问题三：观看以下三个视频后发表你的看法

链接：https：//pan.baidu.com/s/1w05P4nWwskbxRR1K1EorJw提取码：4hrh

设计意图：作为翻转课堂的重要一环，这些指导性问题会帮助学生思考他们所阅读的课本知识，从而引导学生自主探究，提高课堂参与度和有效度。

图3-25　上课前的BB论坛师生互动

2.2　课堂教学

教师授课时，主要通过学生提问来引导课堂的进行，重点在于解决学生面临的关键挑战：为何置信水平可以解释成所有可能样本中，其对应的置信区间包含总体平均值的样本的比例。这最终成为课堂讨论最重要的环节。

对于上述问题极有意义的准备即是置信区间公式的推导过程，也即

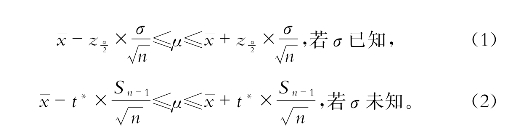(www.xing528.com)

在讲解这两个公式特别是当σ已知时的公式时，我们使用中心极限定理的公式，也即

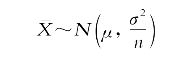
可以得到

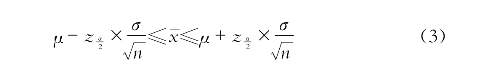
课上教师追问：公式（3）和公式（1）有何区别与联系？从而帮助学生了解公式的来龙去脉。对于公式（1）和公式（3）的转换的理解没有跟上的学生，教师可以进一步通过简单的两点间距离的绝对值不等式来进行讲解，比如，

的意义在于x1与x2的距离小于2，也可以同时理解为x1存在于以x2为中心，以2个单位为半径的范围内，反之亦然。

对于此问题还有理解障碍的学生，教师可以再设计另一种更为直观的场景，通过邀请同学上台参与的游戏化方式，帮助学生理解（本案例由张明欣老师提供）。

一个篮球队有11名队员，现在只选5名队员上场比赛，选拔的流程是：

步骤一：先把所有队员按身高排一排（在班里选11个男生，排成中间高，两边低的队形，面向其他学生。这时其他学生能看到的就是一个模拟出来的单峰对称的分布。从左到右记这些学生为ABCDEFGHIJK）。

步骤二：选择核心队员（假定队里任何一人都可以成为核心队员），该队员举手示意。然后基于此核心队员，选择他左右两边的各两名同学，由此组成五人队伍。例如，若核心队员为F，则DEGH会被选上。若核心球员是D，则BCEF会被选上。从直观的队伍中，学生会发现，如果D在以F为核心的队伍里面，那么F也会在以D为核心的队伍里面。

通过这样的课堂游戏，帮助学生理解（1）和（3）的关系。

如果学生对于上述问题都理解得比较好了，老师可以试图再多问几个问题把学生自认为已搞“清”的状态搞“混”，让他们二度进入“烧脑”模式。比如，对置信区间的一种解释说法：一个样本给出的95%置信区间包含总体平均值的概率为0.95。这种说法是否严格呢？要求学生讨论自己的理解。再比如，如果样本大小为整个总体，那么置信区间是什么情况呢？如果置信水平为100%，那么置信区间是什么情况呢？

对于σ未知的情况，老师可以布置对t-分布的探究任务，帮助学生更好地理解t-分布。可以引导学生的问题包括：自由度对于t-分布的图像有何影响？探讨t-分布与标准正态分布的联系与区别。使用的在线应用程序截屏如图3-26。

想清楚这个问题的关键在于总体方差的无偏估计：

对于基础较好的学生，考虑差异化教学。

以下是差异化教学的两个可用素材：

在课堂中，可以适时通过“世界人口的身高”问题启发学生对于统计学更加本质意义上的理解，特别是样本与总体关系的理解。通过设问：如果我们已知印度的人口的身高，我们可以给出世界人口的身高的置信区间吗？如果我们已知新西兰人口的身高，所得的世界人口身高的置信区间会不一样吗？同时可以提供一些关于世界人口数据的网站供学生研究、讨论。

所有例题、练习题在课堂上都没有进行细致的讲解，要求学生进行自主学习，通过做作业巩固，并安排在合适的时候进行测试以加强对概念的理解和对技能的练习。

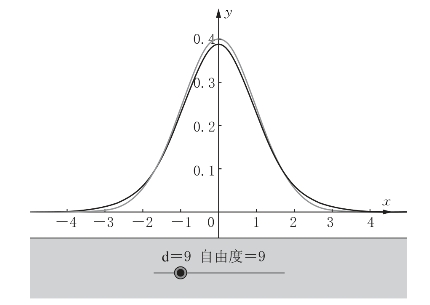
图3-26　t-分布与标准正态分布图像的比较^[15]