1.布置方式
2006版的内部评价与更久远的内部评价版本在布置方式上是雷同的，基本上是采用国际文凭组织官方命题的形式，由学生按照给定的命题，一步步按照既设的方案进行解答。IB组织鼓励IB教师自行命题，但由于自行命题的质量并不一定能够保证学生在各项评价指标上都能够达到最高水平，因此，绝大多数教师自然都要求学生去完成官方的命题。学生对命题的回答不仅仅是给出答案那么简单，而是要用语言文字很好地解说自己的原理、方法和过程，言之有据，形成一篇小型的数学文章。
2.评价标准
评价标准始终是绕不开去的“指挥棒”。2006版的内部评价重视学生语言表达、数学内容及现代技术的使用等。
具体来说，I型要求学生科学地呈现数学过程（包括寻找规律）。要求学生展现其采用的数学策略。学生应科学地收集数据、分析数据，并且能够在得到结论后利用其他例子来测试结论。根据所总结的规律或结构，能够正确地给出一般结论；能够指出一般结论的范围和限制；能够对一般结论规范地进行证明。
II型要求学生定义模型的变量、参数和条件并能正确地分析它们。科学地呈现模型的建立过程，建立适合给定的实际情境并达到该课程水平要求的模型。还应考虑模型对于数据的匹配程度，并把该模型推广到其他情形中去。在合适的精度和给定情境下，正确解释所得结果的合理性。在可能的情况下，能够指出模型的局限性并给出改进的模型。
I型和II型内部评价共通的评分标准如下表2-1、表2-2所示。
表2-1 I型和II型内部评价共通的评分标准（1）
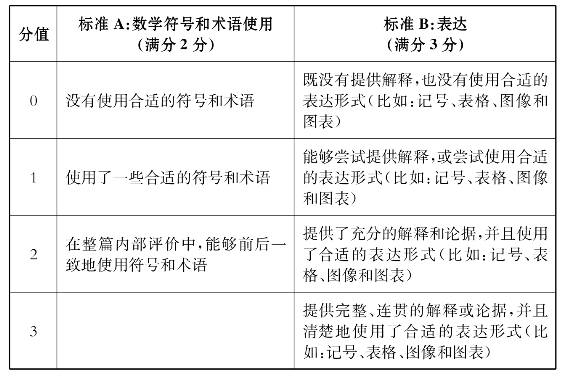
表2-2 I型和II型内部评价共通的评分标准（2）
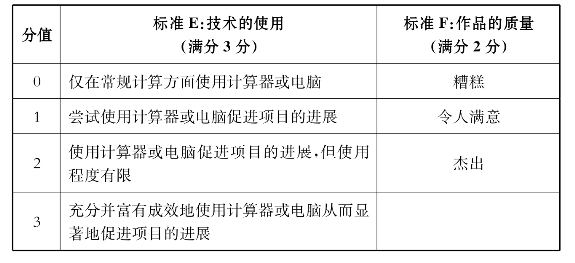
I型内部评价的C项和D项的评分标准如表2-3所示。
表2-3 I型内部评价的C项和D项的评分标准
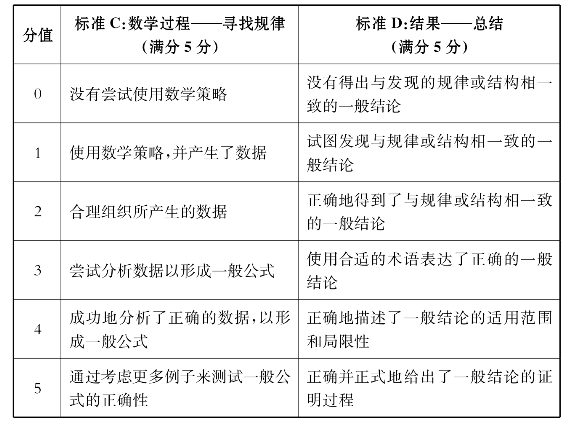
II型内部评价的C项和D项的评分标准如表2-4所示。
表2-4 II型内部评价的C项和D项的评分标准
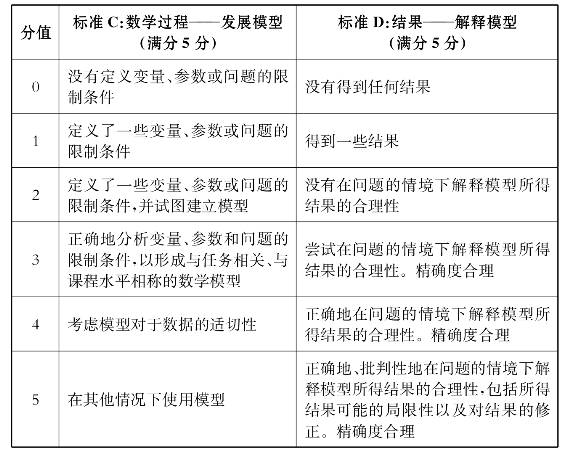
3.实例一则(www.xing528.com)
网球比赛的获胜概率建模（Ⅱ型）
第一部分 俱乐部练习
（1）假设两名运动员经常互相练习，其中Adam的赢球概率一般是Ben赢球概率的两倍。这两个人决定在所在的俱乐部里玩10分的练习。
（a）定义Adam所赢得的分数记为变量X，那么对于这个变量，应用什么概率分布模型比较合适？考虑它的有效性。它的值有没有局限性？
（b）使用你所选择的分布模型，计算随机变量X所有可能的值，使用你的数据画一个直方图。把你用于计算或画图的所有技术都记录下来。
（c）找到这个分布的期望值和标准差。在这个背景下，这些10分的比赛通常会发生什么样的情况？
第二部分 不加长的比赛
（2）当Adam和Ben在俱乐部比赛时，他们的赢球概率和上述大概一致。在俱乐部比赛中，网球比赛的规则基本上适用（每场比赛至少赢4个点，至少比对手多赢2个点），但是为了节省比赛时间，一场比赛不得超过7分。这就意味着如果“平局”出现（每个选手都有3个点），谁得下一个分数就定谁赢。请解释：这样赛制的比赛一共会有70种可能的情况。为了解释清楚，定义变量Y为赢得的点数。变量Y可以取到哪些值？对于每个可能的Y值，给出这个比赛所有可能的结果，并且找出其概率模型。请确保为这个分布定义一个随机变量。
（3）使用你在（2）中得到的模型，求解Adam赢得这场比赛的概率。
（4）总结你的发现。假设选手C和选手D比赛时，选手C得分的概率是c，选手D得分的概率是d。计算选手C赢球的概率。
第三部分 加长的比赛
（5）当Adam和Ben在俱乐部外的锦标赛中比赛时，他们的得分概率依旧保持不变
，但是，比赛规则要求选手必须要多赢两分才算胜利。这样一来，从理论上讲，比赛可能无限延长。请说明，尽管Adam与Ben比赛时赢球的几率是2∶1，Adam赢得比赛的几率几乎是6∶1。请确保分别考虑不打平和打平的比赛。
（6）假设更一般的情况，选手C得分的概率是c，选手D得分的概率是d。请计算如下概率，结果用c和d表示：选手C不到平手即赢得比赛的概率；平局产生的概率；在平局产生的情况下，选手C赢得比赛的概率。使用这些公式帮助计算选手C赢得比赛的概率：c＝0.5，0.55，0.6，0.7，0.9和其他任何你想要测试的数值。鼓励使用电子表格进行计算。
（7）什么样的表达式可以表示那些概率？如果得分的概率互相接近或者一方几乎必定获胜，情况会是怎样？
（8）评价那些概率模型的有用性和局限性。
简评：
这道官方样题激起了很多热爱体育，特别是喜好球类学生的极大兴趣。他们与教师讨论比赛规则的合理性，并利用网络上现成的选手得分情况统计数据。利用这份作业中建立的模型，预测一些重大赛事的结果，以评判自己模型的好坏。不得不感叹的是，这份作业的布置其实也给数学教师提出了要求，那就是教师也需熟悉小球类体育运动及其规则，这样才能更好地与学生交流。
值得注意的是，从这份实例可以清楚地看到，学生不需要规划问题解决的策略和路线，仅需按部就班地执行即可。这是2014年新版内部评价彻底进行改变的着手点。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
