有效投资组合与资本市场线

证券投资组合在降低风险的同时，收益也可能被降低，投资者总是在寻找有效的投资组合。所谓有效组合，是指按既定收益率下风险最小化或既定风险下收益最大化的原则所建立起来的证券组合，如图9-1所示。

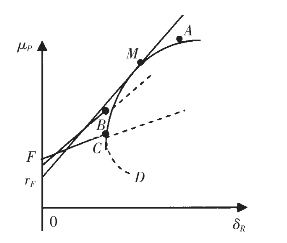
图9-1　投资者共同的最佳组合和有效边界

在图9-1中，曲线AMCD上所有的点表示：当相关系数在-1至+1之间时，A、D两种证券所有可能的不同比重组合；A点表示所有资金全部投在A证券上，D点表示所有资金全部投在D证券上。显然，投资者不会选择CD曲线段上的投资组合，因为在这一段的任意一点，总能找到一个风险水平相同而预期报酬更高的其他投资组合。如M点与D点的风险相同，但预期报酬更高。因此，AMC曲线段是有效投资组合。

有效组合P的预期收益率E（rP）可分成两个部分：一部分是rF，即资金的时间价值；另一部分reδP，则是对所承担的风险δP的奖励，通常称之为风险溢价（风险贴水），它与风险的δP大小成比例。投资者的风险态度决定了三种典型的情况：（1）组合在F点，由无风险证券组成；（2）在FM连续上；（3）在M点以外。

同时，FM射线上的任一有效组合P，与M的相关性为1，记投入无风险证券的资金为x1，则投入市场证券组合的资金为1-x1，有：

rP=x1rF+(1-x1)rM

因为P和M有明显的线性关系，故PPM=1，εP=0，βP=（1-x1）(www.xing528.com)

非系统风险消失，只存在系统风险。这是所有有效组合必须满足的必要条件，若一证券组合存在非系统性风险，它一定不是有效组合。

由投资组合理论可知，如果在证券总体中增加一个可无限买卖的收益率为rF的无风险资产，则在E（r）-δ（r）空间中的有效边界将由双曲线变为一条以（0，rF）为起点的射线，且射线与双曲线顶部相切，如图9-2所示，有效边界由双曲线E1E2变为射线rFM，且两者相切于点M。新的有效边界即射线rFM就是资本市场线CML。由点（0，rF）及斜率，可得资本市场线方程：

图9-2　资本市场线

由上图可知，CML 模型描述的只是处于该线上的投资组合（在此为有效组合）期望收益与标准差的关系，而处于该线以下的证券或投资组合的期望收益与标准差的关系未得到描述。

当市场上不存在无风险资产时，风险证券的有效边界为E1E2，投资者在其上选择哪一点与他对风险的偏好有关；但当市场上存在无风险资产时，有效边界变为射线rFM，投资者虽然可以rFM上根据其风险偏好选择任意一点，但其都将投资于风险证券组合M，这是与其偏好无关的。也即投资者只能在M与无风险资产之间按偏好选择一定的比例，而其投资的风险组合必定是M，这是不依其偏好为转移的。因为如前所述，投资者都是按均值方差准则来选择自己的投资组合的，而新的有效前沿正符合这一条件，若其不在M与无风险资产之间进行选择，那么就不可能在有效前沿上取得自己的位置。只有这样，投资者才能保证其所投资的组合是最优的。这就是投资学上著名的“风险证券投资权数与偏好分离定理”。分离定理的核心在于揭示以下事实：在均衡条件下，每一位投资者只要向风险资产投资则必定持有切点组合；如果切点组合的构造已知，或者有一个切点组合基金，则均衡条件下的投资组合工作大为简化，投资者只需将资金适当分配于无风险资产和切点组合即可实现最佳投资。