证券组合的风险和报酬分析

（一）两种证券的投资组合

假设两种风险性证券A与B，投资者将一定比重的资金投向于A证券，剩余比重的资金投向于B证券。如果R代表证券可能的投资报酬率，E（R）代表投资报酬率的期望值，δ代表证券的标准离差，下标A、B代表不同的证券，下标P表示证券投资组合各种投资报酬情况出现的概率。则有：

组合的期望报酬率 E（RP）=XQE（RA）+XBE（RB）

式中：δAB——两种证券的收益的协方差；

ρAB——两证券收益变动的相关系数。

若ρAB=0，表示两证券的收益完全不相关，一种证券收益的变动不会引起另一种证券收益的相连变化；若ρAB=1，表示两证券的收益完全正相关，一种证券收益的变动会引起另一种证券收益的同向同量变化；若ρAB=-1，表示两证券的收益完全负相关，一种证券收益的变动会引起另一种证券收益的反向同量变化。

上两式表明，投资组合的报酬率（即收益）是构成组合各证券报酬率的加权平均数，但投资组合报酬率的标准差（即风险）并不是构成组合各证券标准差的加权平均数。投资组合能够降低投资风险：只要相关系数ρAB≤1，证券投资组合有可能分散组合中的非系统性风险。

假定两证券的投资风险相等，标准差均为δ，则：

只要ρAB≤1，就有，这表明证券投资组合能降低投资风险。随机地将任何收益非完全正相关的证券组合在一起，都能分散投资风险。

如果ρAB分别取1、0和-1三个数值，则上式转化为：

可见，当相关系数ρ从+1到-1变化时，证券组合的风险逐渐降低；ρ=1时，δP最大，证券组合的风险是各证券风险的加权平均数；ρ=-1时，δP最小。但要使证券组合的风险降低为零，还需要恰当调整投资比例X。

（二）多种证券的投资组合(www.xing528.com)

当投资组合由n 种证券构成时，与两种证券构成的投资组合一样，其收益与风险的关系也由各证券之间的相关性来决定。

假设组合中各证券的报酬率为Ri，投向证券的资本比重为Xi，则：

组合的期望报酬率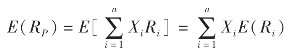

组合的方差

若定义X=（X1，X2，…，Xn）′，R=［E（R1），E（R2），…，E（Rn）］′，并把各证券报酬率之间的协方差矩阵记为：

则投资组合P的期望报酬率和方差可表示为：

〔例9-11〕设有A、B和C三种证券，期望报酬率分别为E（RA）=6%，E（RB）=10%，E（RC）=18%。各证券之间的协方差矩阵为：

如果以这三种证券组成证券投资组合P，并且组合P中各证券的比重分别为X1=0.3，X2=0.4，X3=0.3。有：

组合的期望报酬率E（RP）=X′·R=11.2%

组合的方差

分析结论：证券组合的风险δP取决于三类因素：第一，组合中各类证券所占的比重Xi；第二，各种证券本身的风险δi；第三，各种证券收益之间的相关性ρ。