企业出于交易动机、预防动机、投机动机三者的需要而持有一定的货币,但如何确定最佳现金持有量是现金管理中的重点。现金管理的目标是加快现金的流转速度,压缩闲置现金,以提高现金的获利能力,达到企业利润的最大化。其主要的方法有成本分析模式、存货管理模式、随机模式、现金周转模式。
一般情况下,企业要持有现金,将会出现四种现金成本。
1.现金机会成本。现金作为一项资金占用,是有代价的,这种代价就是现金机会成本。假如某企业的资本成本率为10%,年均持有40万元的现金,则该企业现金每年的现金机会成本为4(=40×10%)万元。现金持有量越大,其机会成本就越高;资本成本率越高,其持有现金的机会成本就越大。企业为了经营业务,需要拥有一定的现金,付出相应的机会成本代价是必要的,但现金拥有量过多,机会成本代价大幅度上升,就不合算了。
2.现金管理成本。企业拥有现金,就必须有设置管理机构,发生管理费用,要支付管理人员工资、安全措施费等等。现金管理成本是一种固定成本,不会随现金持有量的变化而变化,因而现金管理成本是决策的非相关成本。
3.现金短缺成本。现金的短缺成本,是因企业缺乏必要的现金,不能应付业务开支需要,而使企业蒙受经济损失或为此付出的代价。现金的短缺成本会随现金持有量的增加而下降,随现金持有量的减少而上升。
4.现金转换成本。现金转换成本是指企业用现金购入有价证券以及转让有价证券换取现金时付出的交易费用。即现金同有价证券相互转换的成本,如佣金、手续费等。
(一)成本分析模式
成本分析模式是通过分析持有现金的相关成本,寻求总成本最低的现金持有量,如图7-1所示。现金机会成本是一条向右上方倾斜的直线,现金短缺成本是一条向右下方倾斜的曲线,而现金管理成本是一条平行于横轴的直线,总成本是一条抛物线,现金机会成本、现金管理成本和现金短缺成本之和最小的是最佳现金持有量。图上抛物线最低点做出的虚线与横轴相交点(A)就是最佳现金持有量。在A点之前,是现金短缺成本线在现金机会成本线之上,说明了现金短缺成本上升的代价会大于现金机会成本的下降;超越A点之后,现金机会成本上升的代价会大于现金短缺成本的下降。在决策时,管理成本作为不相关成本,可不予考虑。

图7-1 成本分析模式
〔例7-1〕某企业有四种现金持有方案,它们各自的机会成本率和现金短缺成本如表7-1所示。
表7-1 本企业现金持有方案 单位:元

则这四种方案的现金总成本计算结果如表7-2所示。
表7-2 本企业持有现金总成本
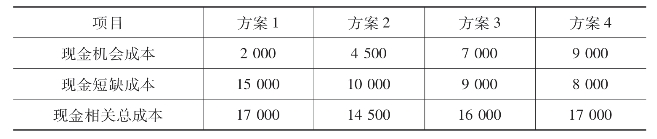
通过以上各方案的现金总成本对比可知,方案2的现金总成本最低,也就是说,当企业持有的现金量是45 000元时,各方面的现金成本总代价最低,对企业最合算,所以45 000元是该企业的最佳现金持有量。
(二)存货管理模式
存货管理模式是指运用企业存货的经济订货量所花费的总成本最低的一次订货量成本管理现金的方法。
从图7-1可知,在最佳现金持有点之前,企业持有过多的现金,会降低现金的短缺成本,但会增加现金占用的现金机会成本;在最佳现金持有点之后,企业没有多余的现金,则会降低现金占用的现金机会成本,增加现金的短缺成本。市场经济中出现了现金的替代品——有价证券,企业存在现金持有过多时,可买入有价证券;当现金短缺时,可卖出有价证券,以避免现金短缺成本的发生,同时又能减少现金机会成本。但是,有价证券与现金的频繁转换是要付出代价的。因此,确定有价证券与现金之间的每次转换量和转换次数是需要考虑的所谓“花费的总成本”。1952年由美国经济学家威廉·鲍曼提出的鲍曼模型就是借用存货的经济订货批量来确定企业的最佳现金持有量的存货模型。
现金的转换成本是与现金转换次数、每次的转换量相关。因为现金每次的转换成本是固定的,企业在一定时期内现金使用量确定的情况下,每次转换量越大,则转换次数越少,转换成本就越低;每次转换量越小,则转换次数越多,转换成本就越高。可见,转换成本的性质与现金短缺成本是一致的,都是与现金的持有量成反比,其成本构成如图7-2所示。

图7-2 最佳现金余额
假设TC为现金的总成本,F1固定为转换成本,T为现金需求总量,Q为最佳现金持有量,K为有价证券的年利息率,则持有现金的总成本可用如下公式表示:(https://www.xing528.com)

求导后,令TC′=0则
〔例7-2〕某企业预计全年所需的现金需求总量为200 000元,平均每次证券固定变现费用为50元,有价证券的年利息率为10%,要求采用存货模式确定该企业的最佳现金持有量。
根据公式,可计算出该企业的最佳现金持有量Q为:所以,某企业最佳现金持有量为14 142元。

(三)随机模式
随机模式是依据企业的现金支出的随机性和在一定时期内无法确定现金需要量的情况下对现金持有量控制的方法。企业可以根据历史经验和实际需要测算出现金持有量的控制范围。“米勒—欧尔”模型如图7-3所示。当现金量达到控制上限(H线)时,用现金购入有价证券,使现金持有量下降到最优现金返回线(R线);当现金量下降到控制下限(L 线),则抛售有价证券换回现金,使现金持有量回升到最优现金返回线(R线)。

图7-3 “米勒—欧尔”模型
一般而言,现金余额在上下限中变动是属于正常的变化范围。如果用b表示每次证券转换为现金的转换成本,i表示证券的日利息率,δ表示每日现金变化的标准差,计算公式表示为:

式中:b——每次有价证券的固定转换成本;
i——有价证券的日利息率;
δ——预期每日现金余额变化的标准差(可根据历史资料测算)。
〔例7-3〕设某公司持有有价证券的平均年利率为5%,每次有价证券转换成本为50元,公司的现金最低持有量为1 500元,又根据以往经验测算出现金变化的标准差为800元。计算最优现金返回线和现金控制上限。

“随机模式”主要是在对企业的现金未来的需求量和收支不可预知的情况下算出相对的现金变化量。通过计算出的现金平均需求量都比最低总成本分析模式高,其现金持有量则比较保守。
(四)现金周转模式
现金周转模式是指根据企业现金周转期来确定最佳现金持有量的方式。企业的现金周转都要经过货币资金、储备资金、生产资金、成品资金和货币资金,一般情况下,在企业全年现金需求总量一定的情况下,现金周转期越短,现金周转所需天数越短,现金持有量就越小。

其中:应收账款周转期是指应收账款发生到收回应收账款所需时间,应付账款周转期是指收到尚未付款的材料到偿还货款支付现金所需时间,存货周转期是指投入材料到产成品入库所需时间。
〔例7-4〕设某公司的材料采购采用赊购,产品销售采用赊销方式。其应收账款的平均收款天数为60天,应付账款的周转天数为40天,存货平均周转天数为90天,预计2019年企业现金需求量为1 080万元,计算该企业2019年的最佳现金持有量。
现金周转期=60-40+90=110(天)
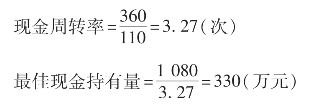
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




