投资组合风险与报酬的评估与优化

投资者想要分散风险，就不宜把全部资金投资到一个项目上去。投资者同时把资金投资于多个投资项目，称为投资组合。项目投资的风险性分析与证券的风险性分析具有一定的可比性，因此，它可以比照证券投资组合的风险与报酬分析。

（一）证券投资组合的报酬率

证券投资组合的报酬率为单项资产预期报酬率的加权平均数，计算公式如下：

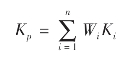
式中：Kp——投资组合预期收益率；

Wi——第i种证券在投资组合总体所占的比重；

Ki——第i种证券预期收益率。

（二）证券投资组合的风险

证券投资组合的风险可以分为两种性质完全不同的风险，即系统风险和非系统风险。

1.非系统风险。非系统风险又叫可分散风险或公司特别风险，是指某些因素对单个证券造成经济损失的可能性。例如，公司在市场竞争中失利等。这种风险，可以通过证券持有的多样化来抵销。至于风险能被分散的程度，则取决于投资组合中不同资产预期报酬之间的相关程度。

“相关”是数列之间相关性的统计计量。如果两个数列的变动沿着相同方向进行，表明它们之间是“正相关”；如果两个数列的变动沿着相反的方向进行，表明它们是“负相关”。相关程度高低用相关系数r来计量，其值位于+1和-1之间。r＞0，表明它们之间正相关，r=+1，为完全正相关；反之，r＜0，表明它们之间负相关，r=-1，为完全负相关。两个数列完全正相关、完全负相关的变动如图3-11和图3-12所示。

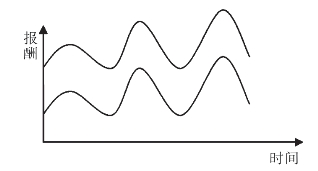
图3-11　两个数列完全正相关变动

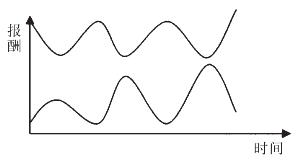
图3-12　两个数列完全负相关变动

现举例说明如下：

假设M股票和N股票构成一证券组合，每种股票在证券组合中各占50%，它们的报酬率和风险情况如表3-2所示。

表3-2　完全负相关的两种股票构成的证券组合收益

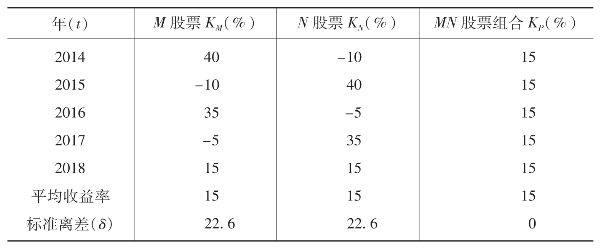
根据表3-2，可以绘制出两种股票及它们构成的证券组合收益图，如图3-13所示。

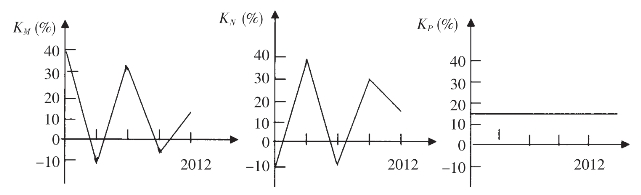
图3-13　两种完全负相关的股票收益图

图中显示，如果投资者单独持有这两种股票，风险都很高，如果把它们形成一个投资组合，则没有风险。其原因是它们完全负相关。

从以上的分析我们知道：（1）当两种完全负相关的股票形成投资组合时，则风险可以完全分散；（2）当两种正相关的股票形成投资组合时，则不能降低任何风险。实际上，各证券之间大部分都是正相关，但不是完全的正相关。就平均而言，其相关系数为+0.6，而大多数股票的相关系数在+0.5～+0.7之间。在这种情况下，把两种股票组合成投资组合能减少风险，但不能消除风险。不过，如果股票数量较多，则能分散掉大部分风险，而当股票数量足够多时，几乎能把所有的非系统风险分散掉。

2.系统风险。系统风险又称为不可分散风险或市场风险，是指那些影响所有公司的因素引起的风险。例如，战争、经济衰退、通货膨胀、高利率等发生意外的、非预期的变动，将影响到所有的证券，不能通过投资组合分散掉。因此，对一个风险充分分散的投资组合来说，重要的是该组合总的风险（系统风险）大小，而不是每一个证券的个别风险（非系统风险）。但是，系统风险对不同的企业也有不同的影响。

不可分散风险的程度，通常用β系数来衡量。β系数反映的是个别证券相对于市场上全部证券平均收益的变动程度。市场收益是指市场上所有证券组成的投资组合收益。从理论上讲，市场投资组合是由所有证券组成的，它的收益率无法确定。但在实际中，通常以一些具有代表性的证券指数作为市场投资组合，再根据证券指数中个别证券的收益率来估计市场投资组合的收益率，然后采用一定的方法来估算β系数，用公式表示如下：

式中：βi——第i项资产的β系数；

Ri——第i项资产的收益率；

ρi，m——第i项资产的收益率与市场组合收益率的相关系数；

δi——该项资产收益率的标准差；

δm——市场组合收益率的标准差；

Rm——市场组合的收益率。

作为整体的证券市场的β系数为1，若某证券的β系数等于1，表明该证券的风险情况与整个证券市场的风险情况一致。若β系数等于0.5，表明该证券的风险只相当于整个证券市场风险的一半，如果整个市场证券平均收益率上升10%，则该证券的收益率只上升5%；如果整个市场证券的平均收益率下降10%，则该证券只下降5%。如果一项证券的β系数等于2，表明该证券的风险情况相当于整个市场证券系统风险的两倍，如果整个市场证券的平均收益率上升10%，则该证券的收益率上升20%；如果整个市场证券的平均收益率下降10%，则该证券下降20%。因此，如果某种证券的β系数大于1，说明其风险大于整个市场风险；如果某种证券的β系数小于1，说明其风险小于整个市场的风险。

β系数作为证券系统风险的量度，在投资分析中有着十分重要的意义，但由于其实际计算过程非常复杂，同时需要大量的数据支持，因此它通常由相当专业的投资服务机构定期计算并公布。2019年11月15日，我国几家上市公司的β系数如表3-3所示。

表3-3　我国几家上市公司的β系数

由几种证券组成的投资组合的β系数，称为加权平均β系数，即以各种证券在投资组合中所占比重为权数，对各个证券的β系数进行加权平均的结果。计算公式如下：

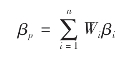
式中：βp——证券投资组合的β系数；

Wi——第i种证券在投资组合中的比重；

βi——投资组合中第i种证券的β系数；(www.xing528.com)

n——投资组合中证券的个数。

有关证券组合的风险归纳如下：

（1）一种股票的风险由两部分组成，即可分散风险和不可分散风险；（2）可分散风险可以通过证券组合来减少；（3）股票的不可分散风险由市场变动而产生，对所有的股票都有影响，不能通过投资组合来消除，不可分散风险是通过β系数来衡量的。证券投资组合风险如图3-14所示。

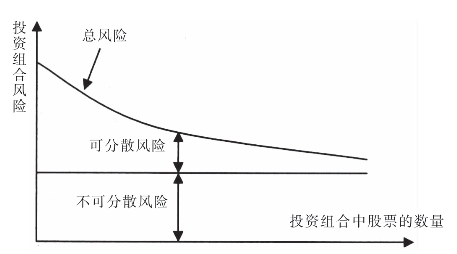
图3-14　证券投资组合风险分析

（三）证券投资组合的风险报酬率

如前所述，投资存在可分散风险和不可分散风险。对于可分散风险，投资者可以通过投资组合加以分散；对于不可分散风险，投资者不可以通过投资组合加以分散，只能靠投资组合的风险报酬加以补偿。因此，投资组合的风险报酬率，就是指投资者因承担不可分散风险而要求的、超过货币时间价值的那部分额外报酬。其计算公式为：

KP=βP(KM-RF)

式中：KP——投资组合的风险报酬率；

βP——投资组合的风险系数；

KM——所有股票的平均报酬率，即市场报酬率；

RF——无风险报酬率。

〔例3-16〕某企业投资组合中有A、B、C三种股票，各自的β系数分别为1.0、1.2、0.8，三种股票所占比重分别为40%、10%、50%，股票市场平均报酬率为15%，无风险报酬率为10%，该企业拟投资200万元，试计算该投资组合的风险报酬率和风险报酬额。

（1）投资组合的β系数：

βP=40%×1.0+10%×1.2+50%×0.8=0.92

（2）投资组合的风险报酬率：

KP=0.92×(15%-10%)=4.6%

（3）投资组合的风险报酬额：

风险报酬额=200×4.6%=9.2（万元）

由以上计算可以看出，在其他因素不变的情况下，风险报酬率的大小主要取决于投资组合的β系数，β系数大，风险报酬率就大，反之亦然。如果调整各种证券在投资组合中的比重，可改变投资组合的β系数，从而改变投资组合的风险报酬率。

（四）证券投资组合风险与报酬的关系

上述风险报酬率的计算是假设投资组合中所有的资产都是风险性资产的前提下，只考虑因承担不可分散风险而要求的、超过时间价值的那部分额外报酬。实际上，投资组合中除风险性资产外，还有大量无风险性资产，如政府债券等。因此，计算投资组合的报酬率必须全面考虑风险与报酬的关系。

资本资产定价模型（Capital Asset Pricing Model，简称CAPM）是西方财务管理学中揭示投资组合风险与报酬之间关系的一个重要模型。这一模型为：

Ki=RF+βi×(RM-RF)

式中：Ki——投资组合中第i种股票的必要报酬率；

RF——无风险报酬率；

βi——投资组合中第i种股票的风险系数；

RM——所有股票的平均报酬率，即市场报酬率。

〔例3-17〕某公司股票的β系数为0.8，无风险报酬率为10%，所有股票的平均报酬率为15%，则该公司的必要报酬率是多少？

Ki=10%+0.8×(15%-10%)=14%

通过计算得知，该公司股票的投资报酬率达到或高于14%的必要报酬率，才值得投资。否则，投资者不会购买该股票。资本资产定价模型也可以用图形来表示，该图形称为证券市场线（SML），它可以用来说明投资组合的必要报酬率Ki与不可分散风险βi系数的关系，如图3-15所示。从图中可以看出，如果无风险报酬率为10%，则β系数不同的股票有不同的风险报酬率，当β=0.8时，风险报酬率为4%；当β=1.0时，风险报酬率为5%；当β=2.0时，风险报酬率为10%。β值越高，要求的风险报酬率越高，在无风险报酬率一定的情况下，必要报酬率就越高。

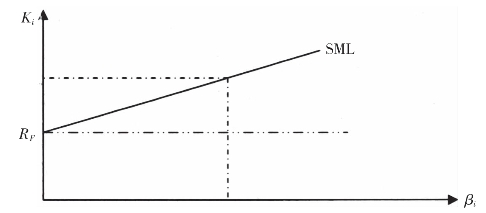
图3-15　证券市场线

从资本资产定价模型和证券市场线可以看出，影响投资者必要报酬率的因素主要有以下三个：

1.无风险报酬率RF。无风险报酬率从投资者的角度看，是最基本的报酬率；从筹资者角度看，是无风险的资本成本。无风险报酬率通常由两部分构成：（1）无通货膨胀的报酬率或真实的报酬率（K0），这是真正的时间价值的部分；（2）通货膨胀贴水（IP），它等于预期的通货膨胀率。可见，通货膨胀对无风险报酬率是有影响的，RF=K0+IP，如图3-16所示，无风险报酬率为RF=10%，它等于8%的真实报酬率和2%的通货膨胀贴水。在其他因素不变的情况下，预期通货膨胀上升3%，引起无风险报酬增加至13%，所有股票的平均报酬率增加3%，证券市场线就会表现为上升。

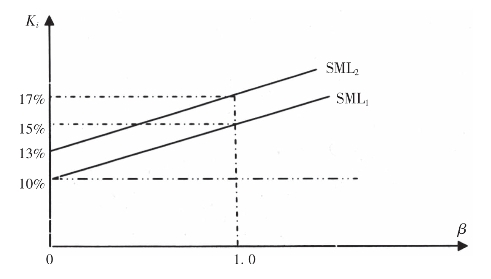
图3-16　通货膨胀与证券报酬

2.市场风险补偿率（KM-RF）。市场风险补偿率是指反映超过无风险报酬率以外的，对投资者承担风险的补偿率。它反映了投资者对风险厌恶的程度，表现为证券市场线的斜率。斜率越大，说明投资者对风险的厌恶程度加深，投资者要求的风险报酬率越大；当斜率为零时，说明投资者不厌恶风险，必要报酬率几乎等于无风险报酬率。风险的厌恶程度如图3-17所示。当市场风险补偿率从5%上升到10%，β=1，风险报酬率从5%上升到10%。风险厌恶程度对β系数较大的股票的影响更为明显，β=0.8时，风险报酬率从4%上升到8%；β=2.0时，风险报酬率从10%上升到20%。

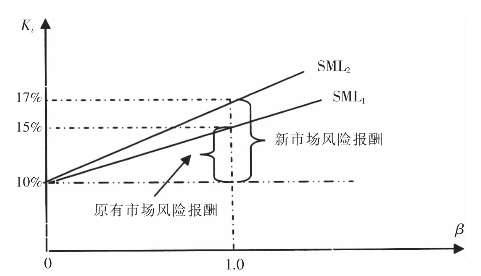
图3-17　市场风险补偿率与证券报酬

3.β系数的变化。β系数可能因企业的资产组合、负债结构等因素发生改变，也会因为市场竞争状况、盈利状况而改变。β系数也可能降低，必要报酬率随之减少。如例3-17中，β系数由0.8上升为2.0，其必要报酬率为：

Ki=10%+2.0×(15%-10%)=20%