历史波动率的估计方法与应用

在本书第五章的B-S公式中提到，利用过去历史股价所求出来的股价报酬波动率，称为历史波动率。其实有很多方法可以利用过去历史的股价数据来估计预期未来股价报酬的波动率。重要的是，看看哪一种估算方法较能正确地预估未来股价的波动率，因此简要介绍几种求算历史波动率的方法。

一、简单加权移动平均法

简单加权移动平均法(equally-weighted moving average)为最常使用的一种方法，第五章第四节也介绍过。此种求法的基本想法是，把每天股价的变动权数看成一样，亦即3个月前股价的变动，跟昨天股价的变动对未来波动率的估算权重是一样的。公式如下:

其中: Rt、分别为每日股价报酬率及平均报酬，N为取样天数，σ为股价报酬的日标准偏差。

将上述的σ乘以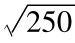，可以转成年化的标准偏差。

二、指数加权移动平均法

由于平均加权把昨天的股价报酬和前1个月某天的股价报酬的权数看成一样，似乎有点不合理。直觉判断，越靠近今天的股价波动，越会影响明天的股价波动，因此，越靠近的日期其权数也应越大。指数加权移动平均法(Exponential Weighted Moving Average，EWMA)就是这种概念。它是摩根银行JP Morgan在其《风险计量》(Risk Metric， 1995)一书中所建议的。其公式如下:

其中: λ是衰退因子(decay factor)，是影响力消逝的速度，λ可能是0.99、0.97或0.94，λ越小表示消逝速度越快。

三、利用每日最高最低的股价来估算

Parkinson(1980)认为，只利用每天收盘价来计算股价报酬的波动率，可能会忽略每天盘中的波动情形，因此，他利用每天最高最低的股价来求波动率，其公式如下:(www.xing528.com)

其中: Ht为当日最高价格，Lt为当日最低价格，ln为自然对数。

对期权而言，股价盘中大幅震荡，也就表示波动增加，相对的也就会影响期权的价格。

四、加入每日开盘收盘价格估算法

Garman and Klass(1981)依照Parkinson所提出的修正，再加入每天的收盘价、开盘价而得，其公式如下:

其中: Ot表示当日开盘价，Ct表示当日收盘价。

五、广义自回归条件异方差法

广义自回归条件异方差法(generalized autoregressive conditional heteroscedasticity， GARCH)由Bollerslev(1986)提出。他认为股价的条件波动率会随着时间改变，大的波动率会紧随大的波动率之后，亦即有波动率群集(volatility clutching)的现象。一般常用Bollerslev的GARCH(1，1)形式，其公式如下:

其中: rt=σtεt，εt～N(0，1)。

公式表示条件变异数σ2t是受最近一期条件变异数σ2t－1及最近一期股价报酬r2t－1的影响;而长期的变异数为，如果α=0，β1=λ，β2=1－λ，则此法即为前面提过的EWMA方法。